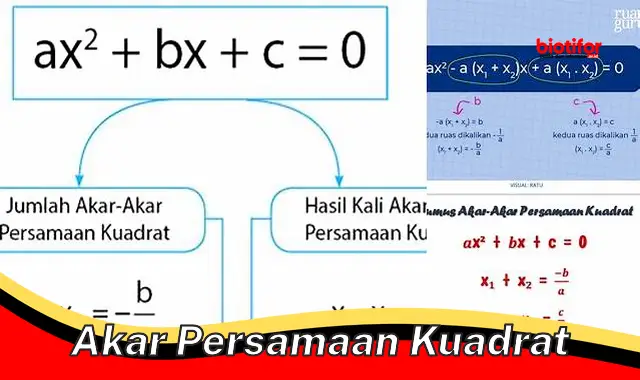
Akar persamaan kuadrat adalah nilai yang memenuhi persamaan kuadrat. Persamaan kuadrat memiliki bentuk umum ax + bx + c = 0, dengan a tidak sama dengan 0. Untuk mencari akar persamaan kuadrat, dapat digunakan rumus kuadrat: x = (-b (b – 4ac)) / 2a. Misalnya, akar persamaan kuadrat x – 5x + 6 = 0 adalah x = 2 atau x = 3.
Akar persamaan kuadrat memiliki peran penting dalam matematika. Akar tersebut digunakan untuk menyelesaikan berbagai permasalahan, seperti mencari titik potong grafik fungsi kuadrat, menentukan maksimum atau minimum fungsi kuadrat, serta mencari titik balik fungsi kuadrat. Selain itu, akar persamaan kuadrat juga digunakan dalam berbagai bidang ilmu pengetahuan, seperti fisika, teknik, dan ekonomi.
Dalam artikel ini, kita akan membahas lebih dalam tentang akar persamaan kuadrat. Kita akan mempelajari cara mencari akar persamaan kuadrat, sifat-sifat akar persamaan kuadrat, serta penerapan akar persamaan kuadrat dalam kehidupan sehari-hari.
Akar Persamaan Kuadrat
Akar persamaan kuadrat merupakan aspek penting dalam matematika yang memiliki berbagai dimensi dan aplikasi. Berikut adalah 10 aspek utama tentang akar persamaan kuadrat:
- Rumus Kuadrat
- Diskriminan
- Akar Rasional
- Akar Irasional
- Persamaan Kuadrat Tak Lengkap
- Aplikasi dalam Geometri
- Aplikasi dalam Fisika
- Aplikasi dalam Ekonomi
- Sifat-sifat Akar
- Penerapan dalam Kehidupan Sehari-hari
Rumus kuadrat digunakan untuk mencari akar persamaan kuadrat. Diskriminan menentukan banyaknya dan jenis akar persamaan kuadrat. Akar rasional dan irasional membedakan jenis akar yang dihasilkan. Persamaan kuadrat tak lengkap memiliki bentuk yang tidak standar. Akar persamaan kuadrat memiliki aplikasi luas dalam geometri, fisika, dan ekonomi. Sifat-sifat akar, seperti jumlah dan hasil kali akar, dapat digunakan untuk menyelesaikan permasalahan matematika. Akar persamaan kuadrat juga diterapkan dalam berbagai aspek kehidupan sehari-hari, seperti mencari titik tertinggi atau terendah suatu fungsi.
Rumus Kuadrat
Rumus kuadrat merupakan rumus matematika yang digunakan untuk mencari akar persamaan kuadrat. Persamaan kuadrat memiliki bentuk umum ax^2 + bx + c = 0, dengan a tidak sama dengan 0. Rumus kuadrat digunakan untuk menentukan nilai x yang memenuhi persamaan tersebut.
Rumus kuadrat memiliki peran penting dalam matematika. Rumus ini digunakan untuk menyelesaikan berbagai permasalahan matematika, seperti mencari titik potong grafik fungsi kuadrat, menentukan maksimum atau minimum fungsi kuadrat, serta mencari titik balik fungsi kuadrat. Selain itu, rumus kuadrat juga digunakan dalam berbagai bidang ilmu pengetahuan, seperti fisika, teknik, dan ekonomi.
Salah satu contoh penerapan rumus kuadrat dalam kehidupan nyata adalah untuk menghitung lintasan sebuah bola yang dilempar ke udara. Dengan menggunakan rumus kuadrat, kita dapat menentukan ketinggian bola pada suatu saat tertentu.
Dengan memahami rumus kuadrat dan cara menggunakannya, kita dapat menyelesaikan berbagai permasalahan matematika dan fisika dengan lebih mudah. Rumus kuadrat merupakan salah satu konsep dasar matematika yang sangat penting untuk dikuasai.
Diskriminan
Diskriminan adalah suatu nilai yang menentukan banyaknya dan jenis akar persamaan kuadrat. Diskriminan dilambangkan dengan huruf D dan dihitung dengan rumus D = b^2 – 4ac, dengan a, b, dan c adalah koefisien persamaan kuadrat ax^2 + bx + c = 0.
Diskriminan sangat penting dalam menentukan akar persamaan kuadrat. Nilai diskriminan menentukan apakah persamaan kuadrat memiliki akar real atau akar kompleks. Jika D > 0, maka persamaan kuadrat memiliki dua akar real yang berbeda. Jika D = 0, maka persamaan kuadrat memiliki akar real yang sama (akar tunggal). Jika D < 0, maka persamaan kuadrat tidak memiliki akar real dan memiliki dua akar kompleks konjugat.
Contohnya, persamaan kuadrat x^2 – 5x + 6 = 0 memiliki diskriminan D = (-5)^2 – 4(1)(6) = 1. Karena D > 0, maka persamaan kuadrat tersebut memiliki dua akar real yang berbeda, yaitu x = 2 dan x = 3.
Memahami diskriminan sangat penting untuk menyelesaikan persamaan kuadrat dengan benar. Diskriminan memberikan informasi penting tentang sifat-sifat akar persamaan kuadrat, sehingga kita dapat menggunakan metode yang tepat untuk menyelesaikan persamaan tersebut.
Akar Rasional
Akar rasional adalah akar persamaan kuadrat yang dapat dinyatakan sebagai hasil bagi dua bilangan bulat. Akar rasional penting dalam matematika karena dapat digunakan untuk menyelesaikan persamaan kuadrat dengan mudah dan cepat.
-
Menemukan Akar Rasional
Untuk menemukan akar rasional persamaan kuadrat, kita dapat menggunakan metode coba-coba. Pertama, kita mencari faktor-faktor dari koefisien konstanta (c). Kemudian, kita mencoba setiap faktor sebagai pembilang dan penyebut akar rasional. Jika kita menemukan kombinasi yang menghasilkan akar yang memenuhi persamaan, maka akar tersebut adalah akar rasional.
-
Contoh Akar Rasional
Misalnya, untuk persamaan kuadrat x^2 – 5x + 6 = 0, faktor-faktor dari koefisien konstanta (6) adalah 1, 2, 3, dan 6. Kita mencoba setiap faktor sebagai pembilang dan penyebut akar rasional. Kita menemukan bahwa x = 2 dan x = 3 adalah akar rasional persamaan tersebut.
-
Penerapan Akar Rasional
Akar rasional digunakan dalam berbagai aplikasi matematika, seperti: – Menyelesaikan persamaan kuadrat- Memfaktorkan polinomial- Mencari titik potong grafik fungsi kuadrat- Menentukan maksimum atau minimum fungsi kuadrat
-
Kesimpulan
Akar rasional merupakan aspek penting dari akar persamaan kuadrat. Akar rasional dapat ditemukan menggunakan metode coba-coba dan memiliki berbagai aplikasi dalam matematika. Memahami akar rasional sangat penting untuk menyelesaikan persamaan kuadrat dan menyelesaikan permasalahan matematika lainnya.
Akar Irasional
Akar irasional adalah akar persamaan kuadrat yang tidak dapat dinyatakan sebagai hasil bagi dua bilangan bulat. Akar irasional penting dalam matematika karena menunjukkan bahwa tidak semua akar persamaan kuadrat dapat diselesaikan secara rasional.
-
Sifat Akar Irasional
Akar irasional memiliki sifat-sifat sebagai berikut: – Tidak dapat dinyatakan sebagai hasil bagi dua bilangan bulat- Merupakan bilangan desimal yang tidak berujung dan tidak berulang- Tidak dapat disederhanakan lagi
-
Contoh Akar Irasional
Contoh akar irasional adalah akar dari 2, akar dari 3, dan akar dari 5. Akar-akar ini tidak dapat dinyatakan sebagai hasil bagi dua bilangan bulat dan memiliki nilai desimal yang tidak berujung dan tidak berulang.
-
Penerapan Akar Irasional
Akar irasional digunakan dalam berbagai aplikasi matematika, seperti: – Menyelesaikan persamaan kuadrat- Memfaktorkan polinomial- Mencari titik potong grafik fungsi kuadrat- Menentukan maksimum atau minimum fungsi kuadrat
-
Hubungan dengan Akar Persamaan Kuadrat
Akar irasional dapat muncul sebagai solusi persamaan kuadrat. Misalnya, persamaan kuadrat x^2 – 2 = 0 memiliki akar-akar x = 2 dan x = -2, yang keduanya merupakan akar irasional.
Kesimpulannya, akar irasional merupakan aspek penting dari akar persamaan kuadrat. Akar irasional menunjukkan bahwa tidak semua akar persamaan kuadrat dapat diselesaikan secara rasional. Memahami akar irasional sangat penting untuk menyelesaikan persamaan kuadrat dan menyelesaikan permasalahan matematika lainnya.
Persamaan Kuadrat Tak Lengkap
Persamaan kuadrat tak lengkap merupakan persamaan kuadrat yang tidak memiliki semua suku (konstanta, koefisien x, dan koefisien x^2). Persamaan kuadrat tak lengkap memiliki peran penting dalam matematika karena banyak masalah di dunia nyata yang dapat dimodelkan menggunakan persamaan jenis ini.
-
Memiliki Suku yang Hilang
Salah satu ciri utama persamaan kuadrat tak lengkap adalah hilangnya salah satu suku. Persamaan kuadrat tak lengkap dapat memiliki suku konstanta yang hilang, seperti pada persamaan x^2 + 2x = 0, atau suku koefisien x yang hilang, seperti pada persamaan x^2 = 4.
-
Aplikasi dalam Kehidupan Nyata
Persamaan kuadrat tak lengkap banyak digunakan untuk memodelkan situasi di dunia nyata. Misalnya, persamaan x^2 = 4 dapat digunakan untuk menghitung jarak yang ditempuh oleh benda yang dilempar ke udara, di mana x adalah jarak dan 4 adalah percepatan gravitasi.
-
Menyelesaikan Persamaan
Persamaan kuadrat tak lengkap dapat diselesaikan menggunakan berbagai metode, seperti pemfaktoran, melengkapkan kuadrat, atau menggunakan rumus kuadrat. Metode yang digunakan tergantung pada jenis persamaan dan suku yang hilang.
-
Hubungan dengan Akar Persamaan Kuadrat
Akar persamaan kuadrat tak lengkap adalah nilai-nilai yang memenuhi persamaan tersebut. Akar persamaan kuadrat tak lengkap dapat berupa akar rasional atau akar irasional, tergantung pada jenis persamaan dan suku yang hilang.
Oleh karena itu, persamaan kuadrat tak lengkap sangat penting dalam memahami akar persamaan kuadrat dan dalam menyelesaikan masalah-masalah di dunia nyata yang dapat dimodelkan menggunakan persamaan jenis ini.
Aplikasi dalam Geometri
Akar persamaan kuadrat memiliki peran penting dalam geometri. Akar ini digunakan untuk menyelesaikan berbagai permasalahan geometri, seperti mencari panjang sisi segitiga, menentukan luas lingkaran, dan menghitung volume kubus.
-
Mencari Panjang Sisi Segitiga
Rumus Phytagoras, yang merupakan dasar banyak permasalahan geometri, melibatkan akar persamaan kuadrat. Rumus ini digunakan untuk mencari panjang sisi segitiga siku-siku, di mana akar persamaan kuadrat digunakan untuk menentukan panjang sisi miring.
-
Menentukan Luas Lingkaran
Luas lingkaran dapat dicari menggunakan rumus r, di mana r adalah jari-jari lingkaran. Untuk mencari jari-jari lingkaran yang melalui tiga titik yang diberikan, digunakan persamaan kuadrat yang melibatkan akar persamaan kuadrat.
-
Menghitung Volume Kubus
Volume kubus dapat dihitung menggunakan rumus V = s, di mana s adalah panjang sisi kubus. Untuk mencari panjang sisi kubus yang diagonal ruangnya diketahui, digunakan persamaan kuadrat yang melibatkan akar persamaan kuadrat.
Selain contoh-contoh di atas, akar persamaan kuadrat juga digunakan dalam berbagai aplikasi geometri lainnya, seperti mencari titik potong garis dan lingkaran, menentukan jarak antara dua titik, dan menghitung luas permukaan bangun ruang. Pemahaman tentang akar persamaan kuadrat sangat penting untuk menyelesaikan berbagai permasalahan geometri dengan akurat dan efisien.
Aplikasi dalam Fisika
Akar persamaan kuadrat memiliki peran penting dalam fisika. Akar ini digunakan untuk menyelesaikan berbagai permasalahan fisika, seperti mencari kecepatan benda, menentukan jarak tempuh benda, dan menghitung gaya yang bekerja pada benda.
-
Mencari Kecepatan Benda
Persamaan gerak benda beraturan berubah berbunyi v = u + at, di mana v adalah kecepatan akhir, u adalah kecepatan awal, a adalah percepatan, dan t adalah waktu. Untuk mencari kecepatan akhir benda, digunakan persamaan kuadrat yang melibatkan akar persamaan kuadrat.
-
Menentukan Jarak Tempuh Benda
Persamaan gerak benda beraturan berubah berbunyi s = ut + 1/2at^2, di mana s adalah jarak tempuh, u adalah kecepatan awal, a adalah percepatan, dan t adalah waktu. Untuk mencari jarak tempuh benda, digunakan persamaan kuadrat yang melibatkan akar persamaan kuadrat.
-
Menghitung Gaya yang Bekerja pada Benda
Persamaan dasar dinamika F = ma, di mana F adalah gaya, m adalah massa, dan a adalah percepatan. Untuk mencari gaya yang bekerja pada benda, digunakan persamaan kuadrat yang melibatkan akar persamaan kuadrat.
Selain contoh-contoh di atas, akar persamaan kuadrat juga digunakan dalam berbagai aplikasi fisika lainnya, seperti mencari titik kesetimbangan benda, menentukan momen inersia benda, dan menghitung energi potensial benda. Pemahaman tentang akar persamaan kuadrat sangat penting untuk menyelesaikan berbagai permasalahan fisika dengan akurat dan efisien.
Aplikasi dalam Ekonomi
Akar persamaan kuadrat memiliki peran penting dalam ekonomi. Akar ini digunakan untuk menyelesaikan berbagai permasalahan ekonomi, seperti menentukan titik impas, memaksimalkan keuntungan, dan menghitung tingkat pengembalian investasi.
-
Menentukan Titik Impas
Titik impas adalah titik di mana total pendapatan sama dengan total biaya. Untuk menentukan titik impas, digunakan persamaan kuadrat yang melibatkan akar persamaan kuadrat.
-
Memaksimalkan Keuntungan
Untuk memaksimalkan keuntungan, perusahaan perlu menentukan jumlah produksi yang optimal. Jumlah produksi yang optimal dapat dicari menggunakan persamaan kuadrat yang melibatkan akar persamaan kuadrat.
-
Menghitung Tingkat Pengembalian Investasi
Tingkat pengembalian investasi (ROI) adalah rasio antara keuntungan yang diperoleh dengan biaya investasi. Untuk menghitung ROI, digunakan persamaan kuadrat yang melibatkan akar persamaan kuadrat.
Selain contoh-contoh di atas, akar persamaan kuadrat juga digunakan dalam berbagai aplikasi ekonomi lainnya, seperti menentukan elastisitas permintaan, menghitung inflasi, dan meramalkan tren ekonomi. Pemahaman tentang akar persamaan kuadrat sangat penting untuk menyelesaikan berbagai permasalahan ekonomi dengan akurat dan efisien.
Sifat-sifat Akar
Sifat-sifat akar persamaan kuadrat memainkan peran penting dalam memahami dan menyelesaikan persamaan tersebut. Sifat-sifat ini memberikan informasi penting tentang akar-akar persamaan kuadrat, seperti jumlah, jenis, dan hubungannya satu sama lain.
-
Jumlah Akar
Persamaan kuadrat memiliki dua akar. Akar-akar tersebut dapat berupa akar real atau akar kompleks.
-
Jenis Akar
Akar persamaan kuadrat dapat berupa akar rasional atau akar irasional. Akar rasional dapat dinyatakan sebagai hasil bagi dua bilangan bulat, sedangkan akar irasional tidak dapat dinyatakan sebagai hasil bagi dua bilangan bulat.
-
Hubungan Akar
Jumlah akar persamaan kuadrat sama dengan negatif koefisien x dibagi dengan koefisien x^2. Hasil kali akar persamaan kuadrat sama dengan konstanta dibagi dengan koefisien x^2.
Sifat-sifat akar persamaan kuadrat ini sangat berguna dalam menyelesaikan persamaan kuadrat. Misalnya, sifat jumlah akar dapat digunakan untuk memeriksa apakah persamaan kuadrat memiliki akar real atau tidak. Sifat jenis akar dapat digunakan untuk menentukan apakah akar-akar persamaan kuadrat rasional atau irasional. Sifat hubungan akar dapat digunakan untuk menentukan nilai akar-akar persamaan kuadrat tanpa harus menyelesaikan persamaan tersebut.
Penerapan dalam Kehidupan Sehari-hari
Akar persamaan kuadrat memiliki peran penting dalam kehidupan sehari-hari. Persamaan kuadrat digunakan untuk menyelesaikan berbagai masalah di bidang yang berbeda, seperti matematika, fisika, dan ekonomi. Dalam kehidupan sehari-hari, akar persamaan kuadrat dapat digunakan untuk:
- Menghitung jarak tempuh kendaraan
- Menentukan titik impas dalam bisnis
- Meramalkan tren ekonomi
- Menghitung tinggi bangunan
- Menemukan titik potong grafik fungsi kuadrat
Memahami akar persamaan kuadrat sangat penting untuk menyelesaikan masalah-masalah ini secara akurat dan efisien. Misalnya, dalam menghitung jarak tempuh kendaraan, persamaan kuadrat digunakan untuk menentukan hubungan antara jarak, kecepatan, dan waktu. Dengan menggunakan akar persamaan kuadrat, kita dapat menghitung jarak tempuh kendaraan untuk waktu tertentu.
Dengan demikian, akar persamaan kuadrat memiliki penerapan yang luas dalam kehidupan sehari-hari. Memahami akar persamaan kuadrat memungkinkan kita untuk menyelesaikan masalah-masalah praktis secara akurat dan efisien.
FAQ tentang Akar Persamaan Kuadrat
Bagian ini akan menjawab beberapa pertanyaan umum tentang akar persamaan kuadrat. Pertanyaan-pertanyaan ini akan memberikan pemahaman yang lebih dalam tentang konsep akar persamaan kuadrat dan penerapannya.
Pertanyaan 1: Apa saja jenis-jenis akar persamaan kuadrat?
Jawaban: Akar persamaan kuadrat dapat berupa akar rasional atau akar irasional. Akar rasional dapat dinyatakan sebagai hasil bagi dua bilangan bulat, sedangkan akar irasional tidak dapat dinyatakan sebagai hasil bagi dua bilangan bulat.
Pertanyaan 2: Bagaimana cara menentukan jumlah akar persamaan kuadrat?
Jawaban: Jumlah akar persamaan kuadrat sama dengan negatif koefisien x dibagi dengan koefisien x^2.
Pertanyaan 3: Apa itu diskriminan dan bagaimana cara menggunakannya?
Jawaban: Diskriminan adalah nilai yang digunakan untuk menentukan jumlah dan jenis akar persamaan kuadrat. Diskriminan dihitung dengan rumus D = b^2 – 4ac, di mana a, b, dan c adalah koefisien persamaan kuadrat ax^2 + bx + c = 0.
Pertanyaan 4: Bagaimana cara menyelesaikan persamaan kuadrat yang memiliki akar irasional?
Jawaban: Persamaan kuadrat yang memiliki akar irasional tidak dapat diselesaikan secara rasional. Namun, kita dapat memperkirakan nilai akar irasional tersebut menggunakan metode numerik, seperti metode bagi dua atau metode Newton-Raphson.
Pertanyaan 5: Apa saja penerapan akar persamaan kuadrat dalam kehidupan sehari-hari?
Jawaban: Akar persamaan kuadrat memiliki banyak penerapan dalam kehidupan sehari-hari, seperti menghitung jarak tempuh kendaraan, menentukan titik impas dalam bisnis, meramalkan tren ekonomi, menghitung tinggi bangunan, dan menemukan titik potong grafik fungsi kuadrat.
Pertanyaan 6: Mengapa penting untuk memahami akar persamaan kuadrat?
Jawaban: Memahami akar persamaan kuadrat sangat penting karena memungkinkan kita untuk menyelesaikan masalah-masalah matematika, fisika, dan ekonomi secara akurat dan efisien. Akar persamaan kuadrat juga memberikan informasi penting tentang sifat-sifat persamaan kuadrat, seperti jumlah, jenis, dan hubungan akar-akarnya.
Dengan memahami konsep akar persamaan kuadrat dan penerapannya, kita dapat menyelesaikan berbagai masalah di berbagai bidang dengan lebih efektif.
Transisi ke bagian artikel selanjutnya:
Selain memahami akar persamaan kuadrat, penting juga untuk memahami sifat-sifat persamaan kuadrat secara umum. Bagian selanjutnya akan membahas sifat-sifat persamaan kuadrat dan penerapannya dalam menyelesaikan masalah.
Tips Memahami Akar Persamaan Kuadrat
Memahami akar persamaan kuadrat sangat penting untuk menyelesaikan berbagai permasalahan matematika, fisika, dan ekonomi. Berikut adalah beberapa tips untuk membantu Anda memahami akar persamaan kuadrat:
Tip 1: Pahami Konsep Dasar
Sebelum mempelajari akar persamaan kuadrat, pastikan Anda memahami konsep dasar persamaan kuadrat, seperti bentuk umum, koefisien, dan diskriminan.
Tip 2: Gunakan Rumus Kuadrat
Rumus kuadrat adalah rumus umum yang dapat digunakan untuk menyelesaikan persamaan kuadrat. Rumus ini akan memberikan dua nilai akar, yang dapat berupa akar real atau kompleks.
Tip 3: Perhatikan Diskriminan
Diskriminan adalah nilai yang menentukan jumlah dan jenis akar persamaan kuadrat. Diskriminan positif menunjukkan dua akar real, diskriminan nol menunjukkan satu akar real (akar tunggal), dan diskriminan negatif menunjukkan dua akar kompleks.
Tip 4: Latih Soal-soal
Cara terbaik untuk memahami akar persamaan kuadrat adalah dengan berlatih menyelesaikan soal-soal. Carilah soal-soal latihan yang bervariasi, mulai dari soal yang mudah hingga soal yang lebih kompleks.
Tip 5: Terapkan dalam Masalah Nyata
Akar persamaan kuadrat memiliki banyak penerapan dalam kehidupan nyata. Cobalah untuk mencari masalah-masalah yang dapat diselesaikan menggunakan persamaan kuadrat, seperti menghitung jarak tempuh kendaraan atau menentukan titik impas dalam bisnis.
Dengan mengikuti tips-tips ini, Anda dapat meningkatkan pemahaman Anda tentang akar persamaan kuadrat dan menerapkannya untuk menyelesaikan berbagai masalah dengan lebih efektif.
Transisi ke bagian artikel selanjutnya:
Selain memahami akar persamaan kuadrat, penting juga untuk memahami sifat-sifat persamaan kuadrat secara umum. Bagian selanjutnya akan membahas sifat-sifat persamaan kuadrat dan penerapannya dalam menyelesaikan masalah.
Kesimpulan
Akar persamaan kuadrat merupakan konsep penting dalam matematika yang memiliki berbagai aplikasi dalam berbagai bidang ilmu pengetahuan dan kehidupan sehari-hari. Pemahaman tentang akar persamaan kuadrat sangat penting untuk menyelesaikan masalah-masalah yang melibatkan fungsi kuadrat, seperti mencari titik potong, menentukan maksimum atau minimum, dan menyelesaikan persamaan kuadrat.
Artikel ini telah membahas secara komprehensif tentang akar persamaan kuadrat, mulai dari definisi, sifat-sifat, metode penyelesaian, hingga penerapannya. Dengan memahami konsep ini secara mendalam, kita dapat menyelesaikan masalah-masalah matematika dan fisika dengan lebih efektif, serta membuat prediksi dan peramalan dalam berbagai bidang ilmu pengetahuan dan kehidupan nyata.
Youtube Video:
