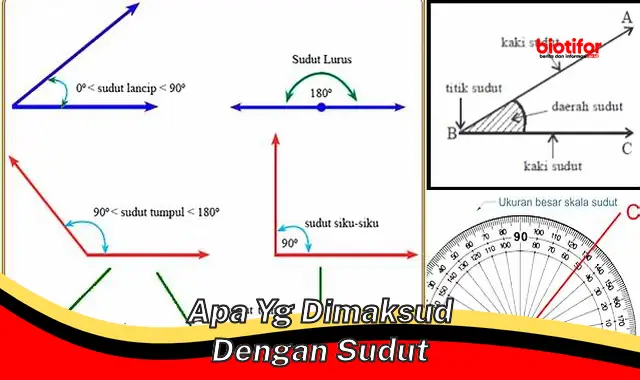
Sudut adalah besaran yang menyatakan besarnya bidang datar yang dibentuk oleh dua garis yang berpotongan pada suatu titik yang disebut titik sudut. Sudut diukur dalam derajat, menit, dan detik.
Sudut sangat penting dalam geometri dan trigonometri. Sudut digunakan untuk mengukur besarnya segitiga, mencari panjang sisi segitiga, dan menentukan posisi suatu titik pada bidang kartesius.
Dalam kehidupan sehari-hari, sudut juga banyak ditemui. Misalnya, sudut kemiringan jalan, sudut pandang mata, dan sudut putaran roda kendaraan.
apa yg dimaksud dengan sudut
Sudut merupakan besaran yang penting dalam matematika dan memiliki berbagai aspek yang perlu dipahami.
- Ukuran bidang datar
- Dibentuk oleh dua garis
- Titik potong disebut titik sudut
- Besaran sudut diukur dalam derajat
- Digunakan dalam geometri dan trigonometri
- Menentukan ukuran segitiga
- Menentukan panjang sisi segitiga
- Menentukan posisi titik pada bidang kartesius
- Digunakan dalam kehidupan sehari-hari
- Contoh: sudut kemiringan jalan, sudut pandangan mata
Memahami aspek-aspek sudut sangat penting dalam matematika dan memiliki aplikasi yang luas dalam kehidupan sehari-hari. Dengan memahami konsep sudut, kita dapat menyelesaikan masalah-masalah matematika dengan lebih mudah dan memahami fenomena alam yang terjadi di sekitar kita.
Ukuran bidang datar
Ukuran bidang datar merupakan salah satu aspek penting dalam konsep sudut. Bidang datar yang dimaksud adalah bidang yang terbentuk oleh dua garis yang berpotongan pada suatu titik. Ukuran bidang datar ini menentukan besarnya sudut yang dibentuk.
Semakin besar bidang datar yang terbentuk, semakin besar pula sudut yang terbentuk. Sebaliknya, semakin kecil bidang datar yang terbentuk, semakin kecil pula sudut yang terbentuk.
Dalam kehidupan sehari-hari, konsep ukuran bidang datar dan sudut ini banyak ditemui. Misalnya, pada roda kendaraan. Besarnya sudut putaran roda menentukan seberapa besar bidang datar yang dilalui roda tersebut. Semakin besar sudut putaran roda, semakin besar pula bidang datar yang dilalui. Sebaliknya, semakin kecil sudut putaran roda, semakin kecil pula bidang datar yang dilalui.
Memahami hubungan antara ukuran bidang datar dan sudut sangat penting dalam berbagai bidang, seperti matematika, fisika, dan teknik. Dengan memahami konsep ini, kita dapat menyelesaikan masalah-masalah yang berkaitan dengan sudut dan bidang datar dengan lebih mudah dan akurat.
Dibentuk oleh dua garis
Sudut terbentuk oleh dua garis yang berpotongan pada suatu titik. Garis-garis tersebut disebut kaki sudut, sedangkan titik potongnya disebut titik sudut.
-
Jenis-jenis sudut
Berdasarkan besarnya, sudut dapat dibagi menjadi beberapa jenis, antara lain:
- Sudut lancip: sudut yang besarnya kurang dari 90 derajat
- Sudut siku-siku: sudut yang besarnya tepat 90 derajat
- Sudut tumpul: sudut yang besarnya lebih dari 90 derajat tetapi kurang dari 180 derajat
- Sudut lurus: sudut yang besarnya tepat 180 derajat
-
Pengukuran sudut
Besar sudut dapat diukur menggunakan berbagai satuan, antara lain:
- Derajat
- Menit
- Detik
-
Aplikasi sudut
Sudut memiliki banyak aplikasi dalam kehidupan sehari-hari, antara lain:
- Arsitektur
- Teknik sipil
- Navigasi
- Astronomi
Dengan memahami konsep sudut dan hubungannya dengan garis, kita dapat memahami berbagai fenomena alam dan menyelesaikan berbagai masalah matematika dengan lebih mudah.
Titik potong disebut titik sudut
Dalam definisi sudut, titik potong dua garis yang membentuk sudut disebut titik sudut. Titik sudut merupakan komponen penting dalam konsep sudut karena menjadi acuan dalam menentukan besar sudut.
Tanpa adanya titik sudut, sudut tidak dapat terbentuk. Dua garis yang saling berpotongan akan membentuk dua sudut yang berhadapan, dengan titik potong sebagai titik sudutnya.
Memahami konsep titik sudut sangat penting dalam mempelajari sudut. Titik sudut menjadi dasar dalam pengukuran sudut, pembagian jenis-jenis sudut, serta aplikasi sudut dalam berbagai bidang.
Besaran sudut diukur dalam derajat
Besaran sudut merupakan salah satu aspek penting dalam memahami konsep sudut. Sudut diukur menggunakan satuan derajat, yang merupakan satuan standar untuk mengukur besar sudut.
Derajat digunakan untuk menentukan besar sudut karena memiliki nilai yang mudah dipahami dan digunakan dalam berbagai aplikasi. Satu derajat didefinisikan sebagai 1/360 bagian dari satu putaran penuh.
Pengukuran sudut dalam derajat sangat penting dalam berbagai bidang, seperti matematika, fisika, dan teknik. Dalam matematika, derajat digunakan untuk mengukur besar sudut segitiga, menentukan posisi titik pada bidang kartesius, dan menyelesaikan berbagai masalah geometri.
Dalam fisika, derajat digunakan untuk mengukur sudut putaran benda, sudut datang dan sudut pantul cahaya, serta berbagai besaran fisika lainnya. Dalam teknik, derajat digunakan untuk mengukur sudut kemiringan jalan, sudut putaran roda, dan sudut kemudi kendaraan.
Memahami hubungan antara besaran sudut dan derajat sangat penting untuk memahami berbagai fenomena alam dan menyelesaikan berbagai masalah matematika dan teknik. Dengan memahami konsep ini, kita dapat mengukur dan menentukan besar sudut dengan lebih mudah dan akurat.
Digunakan dalam geometri dan trigonometri
Konsep sudut memegang peranan penting dalam geometri dan trigonometri. Sudut digunakan untuk mengukur dan menghitung berbagai aspek bangun datar dan bangun ruang, serta untuk menyelesaikan permasalahan yang melibatkan besaran sudut.
-
Mengukur besar segitiga
Dalam geometri, sudut digunakan untuk mengukur besar segitiga. Besar sudut sebuah segitiga dapat digunakan untuk menentukan jenis segitiga tersebut, seperti segitiga siku-siku, segitiga lancip, atau segitiga tumpul.
-
Mencari panjang sisi segitiga
Selain mengukur besar segitiga, sudut juga dapat digunakan untuk mencari panjang sisi segitiga. Dengan menggunakan konsep trigonometri, panjang sisi segitiga dapat ditentukan jika diketahui besar dua sudut dan panjang satu sisi.
-
Menentukan posisi titik pada bidang kartesius
Dalam trigonometri, sudut digunakan untuk menentukan posisi titik pada bidang kartesius. Posisi titik pada bidang kartesius dapat ditentukan dengan menggunakan konsep sudut dan fungsi trigonometri.
-
Menghitung besaran fisika
Selain dalam geometri, sudut juga digunakan dalam trigonometri untuk menghitung berbagai besaran fisika, seperti kecepatan, percepatan, dan gaya. Dengan menggunakan konsep sudut dan fungsi trigonometri, besaran-besaran fisika tersebut dapat dihitung dengan lebih mudah dan akurat.
Dengan demikian, konsep sudut sangat penting dalam geometri dan trigonometri, karena digunakan untuk mengukur besar segitiga, mencari panjang sisi segitiga, menentukan posisi titik pada bidang kartesius, dan menghitung berbagai besaran fisika. Pemahaman yang baik tentang sudut sangat penting untuk keberhasilan dalam mempelajari geometri dan trigonometri.
Menentukan ukuran segitiga
Sudut memegang peranan penting dalam menentukan ukuran segitiga. Ukuran segitiga ditentukan oleh panjang sisi-sisinya dan besar sudut-sudutnya. Dalam geometri, terdapat beberapa teorema dan rumus yang digunakan untuk menentukan ukuran segitiga berdasarkan sudut dan sisi-sisinya.
-
Teorema Pythagoras
Teorema Pythagoras menyatakan bahwa pada segitiga siku-siku, kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang kedua sisi lainnya. Rumus Teorema Pythagoras adalah:
c = a + b
dengan c adalah sisi miring dan a dan b adalah kedua sisi lainnya. -
Trigonometri
Trigonometri adalah cabang matematika yang mempelajari hubungan antara sudut dan sisi segitiga. Dalam trigonometri, terdapat fungsi trigonometri seperti sinus, kosinus, dan tangen yang dapat digunakan untuk menentukan panjang sisi atau besar sudut segitiga jika diketahui beberapa nilai lainnya. -
Rumus Heron
Rumus Heron digunakan untuk menentukan luas segitiga jika diketahui panjang ketiga sisinya. Rumus Heron adalah:
Luas = s(s-a)(s-b)(s-c)
dengan s adalah setengah keliling segitiga dan a, b, c adalah panjang ketiga sisinya. -
Sifat-sifat segitiga
Selain menggunakan teorema dan rumus, menentukan ukuran segitiga juga dapat dilakukan dengan memanfaatkan sifat-sifat segitiga. Misalnya, jumlah besar sudut dalam segitiga selalu sama dengan 180 derajat, dan jumlah panjang kedua sisi segitiga selalu lebih besar dari panjang sisi lainnya.
Dengan memahami hubungan antara sudut dan ukuran segitiga, kita dapat menentukan ukuran segitiga dengan lebih mudah dan akurat. Konsep ini sangat penting dalam berbagai bidang, seperti arsitektur, teknik sipil, dan navigasi.
Menentukan panjang sisi segitiga
Dalam geometri, sudut memegang peranan penting dalam menentukan panjang sisi segitiga. Konsep sudut digunakan dalam berbagai teorema dan rumus untuk menghitung panjang sisi segitiga jika diketahui besar sudut dan panjang sisi lainnya.
-
Teorema Pythagoras
Teorema Pythagoras menyatakan bahwa pada segitiga siku-siku, kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang kedua sisi lainnya. Rumus Teorema Pythagoras dapat digunakan untuk menentukan panjang sisi miring jika diketahui panjang kedua sisi lainnya, atau sebaliknya. -
Trigonometri
Trigonometri adalah cabang matematika yang mempelajari hubungan antara sudut dan sisi segitiga. Fungsi trigonometri, seperti sinus, kosinus, dan tangen, dapat digunakan untuk menentukan panjang sisi segitiga jika diketahui besar dua sudut dan panjang satu sisi. -
Sifat-sifat segitiga
Sifat-sifat segitiga, seperti jumlah besar sudut dalam segitiga selalu sama dengan 180 derajat, juga dapat digunakan untuk menentukan panjang sisi segitiga. Misalnya, jika diketahui besar dua sudut dan panjang satu sisi, panjang sisi lainnya dapat ditentukan menggunakan sifat sudut dalam segitiga.
Dengan memahami hubungan antara sudut dan panjang sisi segitiga, kita dapat menentukan ukuran segitiga dengan lebih mudah dan akurat. Konsep ini sangat penting dalam berbagai bidang, seperti arsitektur, teknik sipil, dan navigasi.
Menentukan posisi titik pada bidang kartesius
Posisi titik pada bidang kartesius ditentukan oleh koordinatnya, yaitu jarak titik tersebut dari sumbu x dan sumbu y. Untuk menentukan koordinat suatu titik, diperlukan konsep sudut.
-
Sudut antara garis yang menghubungkan titik dengan sumbu x dan sumbu x
Sudut ini digunakan untuk menentukan kuadran di mana titik tersebut berada. -
Sudut antara garis yang menghubungkan titik dengan titik asal dan sumbu x
Sudut ini digunakan untuk menentukan koordinat x titik tersebut. -
Sudut antara garis yang menghubungkan titik dengan titik asal dan sumbu y
Sudut ini digunakan untuk menentukan koordinat y titik tersebut.
Dengan memahami hubungan antara sudut dan posisi titik pada bidang kartesius, kita dapat menentukan posisi titik dengan lebih mudah dan akurat. Konsep ini sangat penting dalam berbagai bidang, seperti matematika, fisika, dan teknik.
Digunakan dalam kehidupan sehari-hari
Konsep sudut banyak digunakan dalam kehidupan sehari-hari, baik secara sadar maupun tidak sadar. Pemahaman tentang sudut sangat penting untuk memahami dan memecahkan berbagai masalah yang dihadapi dalam kehidupan sehari-hari.
-
Pengukuran dan estimasi
Sudut digunakan dalam berbagai alat ukur, seperti busur derajat, klinometer, dan sextant. Alat-alat ini digunakan untuk mengukur sudut benda atau kemiringan permukaan. Selain itu, sudut juga digunakan dalam estimasi, seperti memperkirakan sudut belok saat berkendara atau sudut kemiringan lereng. -
Desain dan konstruksi
Sudut sangat penting dalam desain dan konstruksi. Arsitek dan insinyur menggunakan sudut untuk menentukan kemiringan atap, sudut tangga, dan sudut sambungan antar bagian bangunan. Sudut juga digunakan dalam pertukangan dan pekerjaan logam untuk membuat potongan dan sambungan yang presisi. -
Navigasi dan transportasi
Sudut digunakan dalam navigasi untuk menentukan arah dan posisi. Kompas menggunakan sudut untuk menunjukkan arah utara, dan GPS menggunakan sudut untuk menentukan posisi di bumi. Sudut juga digunakan dalam transportasi untuk menentukan sudut kemudi kendaraan dan sudut belok. -
Olahraga dan permainan
Sudut sangat penting dalam berbagai olahraga dan permainan. Dalam sepak bola, sudut digunakan untuk menentukan sudut tendangan bebas dan tendangan sudut. Dalam golf, sudut digunakan untuk menentukan sudut ayunan dan arah bola. Sudut juga digunakan dalam permainan biliar dan snooker untuk menentukan arah dan kecepatan bola.
Dari contoh-contoh di atas, dapat dilihat bahwa konsep sudut memiliki aplikasi yang luas dalam kehidupan sehari-hari. Memahami konsep sudut sangat penting untuk memahami dan memecahkan berbagai masalah yang dihadapi dalam berbagai bidang, mulai dari pengukuran dan estimasi hingga desain, konstruksi, navigasi, transportasi, olahraga, dan permainan.
Contoh
Sudut kemiringan jalan dan sudut pandangan mata merupakan contoh nyata dari penerapan konsep sudut dalam kehidupan sehari-hari. Sudut kemiringan jalan menentukan tingkat kecuraman jalan, yang penting untuk keselamatan berkendara dan pejalan kaki. Sementara itu, sudut pandangan mata menentukan arah dan jangkauan penglihatan kita, yang penting untuk aktivitas sehari-hari seperti berjalan, mengemudi, dan membaca.
Dengan memahami konsep sudut, kita dapat memahami dan mengukur sudut kemiringan jalan dan sudut pandangan mata dengan lebih akurat. Hal ini penting untuk berbagai keperluan, seperti desain jalan yang aman, pemasangan rambu lalu lintas yang efektif, dan optimalisasi sistem pencahayaan. Selain itu, pemahaman tentang sudut juga membantu kita memahami prinsip kerja berbagai alat optik, seperti teropong dan mikroskop.
Secara keseluruhan, memahami hubungan antara konsep sudut dan contoh-contoh nyata seperti sudut kemiringan jalan dan sudut pandangan mata sangat penting untuk berbagai aspek kehidupan sehari-hari. Pemahaman ini memungkinkan kita untuk membuat keputusan yang lebih tepat, menggunakan teknologi secara lebih efektif, dan memahami dunia di sekitar kita dengan lebih baik.
Apa yang dimaksud dengan sudut?
Sudut adalah besaran yang menyatakan besarnya bidang datar yang dibentuk oleh dua garis yang berpotongan pada suatu titik. Sudut diukur dalam derajat, menit, dan detik.
Pertanyaan 1: Apa itu titik sudut?
Jawaban: Titik sudut adalah titik potong dua garis yang membentuk sudut.
Pertanyaan 2: Bagaimana cara mengukur sudut?
Jawaban: Sudut dapat diukur menggunakan busur derajat, klinometer, atau sextant. Satuan yang digunakan untuk mengukur sudut adalah derajat, menit, dan detik.
Pertanyaan 3: Apa saja jenis-jenis sudut?
Jawaban: Jenis-jenis sudut berdasarkan besarnya antara lain sudut lancip (kurang dari 90 derajat), sudut siku-siku (90 derajat), sudut tumpul (lebih dari 90 derajat tetapi kurang dari 180 derajat), dan sudut lurus (180 derajat).
Pertanyaan 4: Di mana saja sudut digunakan dalam kehidupan sehari-hari?
Jawaban: Sudut digunakan dalam berbagai bidang, seperti arsitektur, teknik sipil, navigasi, dan olahraga.
Pertanyaan 5: Mengapa memahami konsep sudut itu penting?
Jawaban: Memahami konsep sudut sangat penting untuk memahami dan memecahkan berbagai masalah yang dihadapi dalam kehidupan sehari-hari. Konsep sudut juga merupakan dasar dari trigonometri, yang merupakan cabang matematika yang mempelajari hubungan antara sudut dan sisi segitiga.
Pertanyaan 6: Bagaimana cara menerapkan konsep sudut dalam kehidupan nyata?
Jawaban: Konsep sudut dapat diterapkan dalam kehidupan nyata dengan cara mengukur sudut kemiringan jalan, menentukan sudut pandangan mata, dan mendesain bangunan dan struktur lainnya.
Dengan memahami konsep sudut dan penerapannya dalam kehidupan nyata, kita dapat memahami dunia di sekitar kita dengan lebih baik dan membuat keputusan yang lebih tepat.
Baca juga: Jenis-jenis sudut dan penerapannya dalam kehidupan sehari-hari.
Tips Memahami Konsep Sudut
Memahami konsep sudut sangat penting untuk berbagai bidang ilmu dan kehidupan sehari-hari. Berikut beberapa tips untuk membantu Anda memahami konsep sudut dengan lebih baik:
Tip 1: Visualisasikan sudut sebagai bidang datar
Bayangkan sudut sebagai bidang datar yang terbentuk oleh dua garis yang berpotongan. Ini akan membantu Anda memahami bahwa sudut mewakili ukuran area, bukan hanya sebuah titik.
Tip 2: Gunakan alat bantu visual
Gunakan alat bantu visual seperti busur derajat atau gambar untuk merepresentasikan sudut secara konkret. Ini akan memudahkan Anda membandingkan besarnya sudut yang berbeda.
Tip 3: Hafalkan jenis-jenis sudut
Pelajari jenis-jenis sudut berdasarkan besarnya, seperti sudut lancip, sudut siku-siku, sudut tumpul, dan sudut lurus. Mengetahui perbedaan antara jenis-jenis sudut akan membantu Anda mengidentifikasi dan mengklasifikasikan sudut dengan cepat.
Tip 4: Terapkan konsep sudut dalam kehidupan nyata
Carilah contoh-contoh sudut dalam kehidupan sehari-hari, seperti sudut kemiringan jalan atau sudut pandangan mata. Ini akan membantu Anda memahami penerapan praktis dari konsep sudut.
Tip 5: Latih soal-soal sudut
Coba kerjakan soal-soal latihan yang melibatkan sudut. Ini akan meningkatkan pemahaman Anda tentang cara mengukur, membandingkan, dan menghitung sudut.
Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman Anda tentang konsep sudut dan menerapkannya secara efektif dalam berbagai konteks.
Baca juga: Aplikasi konsep sudut dalam kehidupan sehari-hari.
Kesimpulan
Sudut merupakan besaran yang sangat penting dalam geometri dan memiliki banyak aplikasi dalam kehidupan sehari-hari. Konsep sudut mencakup berbagai aspek, mulai dari pengertian dasar hingga pengukuran dan penerapannya dalam berbagai bidang.
Memahami konsep sudut sangat penting untuk memahami fenomena alam, menyelesaikan masalah matematika, dan membuat keputusan yang tepat dalam berbagai aspek kehidupan. Dengan menguasai konsep sudut, kita dapat menjelajahi dunia di sekitar kita dengan lebih baik dan berkontribusi dalam berbagai bidang ilmu dan teknologi.
Youtube Video:
