Panduan Lengkap: Memahami Bagian Lingkaran Secara Mendalam

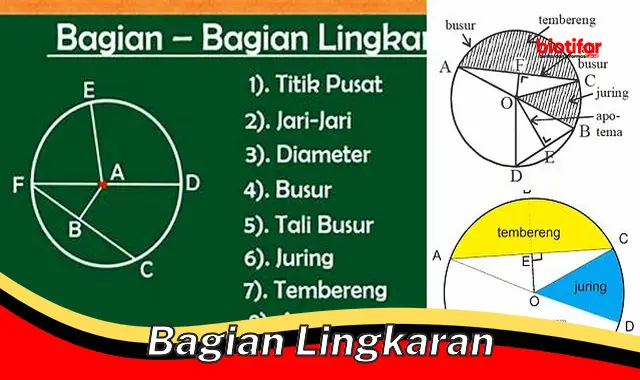
Bagian lingkaran adalah irisan bidang datar dengan bidang lengkung yang dibatasi oleh dua jari-jari dan sebuah busur. Bagian lingkaran dapat berbentuk setengah lingkaran, seperempat lingkaran, atau bentuk lainnya.

Bagian lingkaran memiliki banyak kegunaan dalam kehidupan sehari-hari, seperti:

• Dalam arsitektur, bagian lingkaran digunakan untuk membuat kubah, lengkungan, dan struktur lengkung lainnya.
• Dalam teknik, bagian lingkaran digunakan untuk membuat roda gigi, bantalan, dan komponen mesin lainnya.
• Dalam matematika, bagian lingkaran digunakan untuk menghitung luas dan keliling bangun datar.

Bagian lingkaran juga memiliki sejarah yang panjang. Bangsa Babilonia kuno menggunakan bagian lingkaran untuk menghitung luas dan keliling lingkaran sejak tahun 1900 SM. Bangsa Yunani kuno juga menggunakan bagian lingkaran untuk mengukur sudut dan jarak.

Bagian Lingkaran

Bagian lingkaran merupakan bagian penting dari matematika dan memiliki berbagai aplikasi dalam kehidupan sehari-hari. Berikut adalah 10 aspek penting dari bagian lingkaran:

• Jari-jari
• Busur
• Keliling
• Luas
• Sudut pusat
• Apotema
• Tali busur
• Tangen
• Sekan
• Diameter

Aspek-aspek ini saling berhubungan dan membentuk dasar untuk memahami bagian lingkaran. Misalnya, jari-jari adalah garis yang menghubungkan pusat lingkaran ke sebuah titik pada lingkaran, sedangkan busur adalah bagian dari lingkaran yang dibatasi oleh dua titik. Keliling adalah jarak mengelilingi lingkaran, sedangkan luas adalah ukuran daerah yang dibatasi oleh lingkaran. Sudut pusat adalah sudut yang dibentuk oleh dua jari-jari, sedangkan apotema adalah garis yang menghubungkan pusat lingkaran ke titik tengah tali busur.

Jari-jari

Jari-jari adalah garis yang menghubungkan pusat lingkaran ke sebuah titik pada lingkaran. Dalam konteks bagian lingkaran, jari-jari memiliki beberapa fungsi dan peran penting:

• Menentukan ukuran bagian lingkaran
  Panjang jari-jari menentukan ukuran bagian lingkaran. Bagian lingkaran dengan jari-jari yang lebih panjang akan memiliki keliling dan luas yang lebih besar.
• Membagi bagian lingkaran menjadi dua bagian yang sama
  Dua jari-jari yang digambar dari pusat lingkaran akan membagi bagian lingkaran menjadi dua bagian yang sama besar.
• Menentukan tinggi bagian lingkaran
  Jari-jari yang ditarik tegak lurus terhadap tali busur akan membentuk tinggi bagian lingkaran.
• Menentukan luas bagian lingkaran
  Luas bagian lingkaran dapat dihitung menggunakan rumus: Luas = (r)/2, di mana r adalah panjang jari-jari.

Dengan demikian, jari-jari merupakan komponen penting dari bagian lingkaran yang menentukan ukuran, bentuk, dan sifat-sifat lainnya.

Busur

Busur adalah bagian dari lingkaran yang dibatasi oleh dua titik. Dalam konteks bagian lingkaran, busur memiliki beberapa fungsi dan peran penting:

• Menentukan bentuk bagian lingkaran
  Panjang dan posisi busur menentukan bentuk bagian lingkaran. Bagian lingkaran dapat berbentuk setengah lingkaran, seperempat lingkaran, atau bentuk lainnya, tergantung pada ukuran dan letak busur.
• Menentukan keliling bagian lingkaran
  Keliling bagian lingkaran dapat dihitung menggunakan rumus: Keliling = (2r)/360 x derajat busur, di mana r adalah panjang jari-jari dan derajat busur adalah ukuran busur dalam derajat.
• Menentukan luas bagian lingkaran
  Luas bagian lingkaran dapat dihitung menggunakan rumus: Luas = (r)/360 x derajat busur, di mana r adalah panjang jari-jari dan derajat busur adalah ukuran busur dalam derajat.

Dengan demikian, busur merupakan komponen penting dari bagian lingkaran yang menentukan bentuk, keliling, dan luas bagian lingkaran.

Keliling

Keliling merupakan panjang kurva tertutup yang mengelilingi suatu bangun datar, termasuk bagian lingkaran. Keliling bagian lingkaran memiliki beberapa peran dan keterkaitan penting:

• Mengukur panjang tepi bagian lingkaran
  Keliling digunakan untuk mengukur panjang tepi bagian lingkaran. Keliling bagian lingkaran lebih kecil dari keliling lingkaran penuh, dan bergantung pada besar busur yang membentuk bagian lingkaran.
• Menghitung luas bagian lingkaran
  Keliling bagian lingkaran digunakan dalam menghitung luas bagian lingkaran. Luas bagian lingkaran dapat dihitung dengan rumus: Luas = (1/2) x Keliling x Tinggi, di mana Tinggi adalah jarak dari tali busur ke titik tengah busur bagian lingkaran.
• Menentukan skala dan proporsi bagian lingkaran
  Keliling bagian lingkaran membantu menentukan skala dan proporsi bagian lingkaran. Keliling yang lebih besar menunjukkan bagian lingkaran yang lebih besar, dan sebaliknya.
• Aplikasi dalam kehidupan nyata
  Keliling bagian lingkaran memiliki berbagai aplikasi dalam kehidupan nyata, seperti:
  • Menghitung panjang pagar yang mengelilingi taman berbentuk setengah lingkaran
  • Menghitung keliling roda kendaraan bermotor
  • Menghitung panjang lintasan lari berbentuk seperempat lingkaran

Dengan demikian, keliling merupakan aspek penting dari bagian lingkaran yang digunakan untuk mengukur panjang tepi, menghitung luas, menentukan skala dan proporsi, serta memiliki berbagai aplikasi dalam kehidupan sehari-hari.

Luas

Luas merupakan besaran yang menyatakan ukuran daerah suatu permukaan. Dalam konteks bagian lingkaran, luas memiliki keterkaitan dan peran penting, yaitu:

• Mengukur daerah bagian lingkaran
  Luas digunakan untuk mengukur daerah permukaan bagian lingkaran. Luas bagian lingkaran lebih kecil dari luas lingkaran penuh, dan bergantung pada besar busur yang membentuk bagian lingkaran.
• Menghitung volume bangun ruang
  Luas bagian lingkaran digunakan dalam menghitung volume bangun ruang yang melibatkan bagian lingkaran, seperti kerucut dan bola.
• Menentukan skala dan proporsi bagian lingkaran
  Luas bagian lingkaran membantu menentukan skala dan proporsi bagian lingkaran. Luas yang lebih besar menunjukkan bagian lingkaran yang lebih besar, dan sebaliknya.
• Aplikasi dalam kehidupan nyata
  Luas bagian lingkaran memiliki berbagai aplikasi dalam kehidupan nyata, seperti:
  • Menghitung luas tanah berbentuk setengah lingkaran untuk keperluan pembangunan taman
  • Menghitung luas permukaan bola untuk menentukan kebutuhan cat
  • Menghitung volume air dalam tangki berbentuk kerucut

Dengan demikian, luas merupakan aspek penting dari bagian lingkaran yang digunakan untuk mengukur daerah permukaan, menghitung volume bangun ruang, menentukan skala dan proporsi, serta memiliki berbagai aplikasi dalam kehidupan sehari-hari.

Sudut pusat

Sudut pusat adalah sudut yang dibentuk oleh dua jari-jari lingkaran yang berpotongan di titik pusat. Dalam bagian lingkaran, sudut pusat memiliki peran penting dalam menentukan ukuran dan sifat-sifat bagian lingkaran.

• Membagi bagian lingkaran menjadi beberapa bagian
  Sudut pusat dapat digunakan untuk membagi bagian lingkaran menjadi beberapa bagian yang sama besar. Misalnya, sudut pusat 60 derajat akan membagi setengah lingkaran menjadi tiga bagian yang sama besar.
• Menentukan panjang busur
  Besar sudut pusat berbanding lurus dengan panjang busur yang terbentuk. Sudut pusat yang lebih besar akan menghasilkan busur yang lebih panjang, dan sebaliknya.
• Menghitung luas bagian lingkaran
  Luas bagian lingkaran dapat dihitung menggunakan rumus: Luas = (r²/2) x sudut pusat, di mana r adalah jari-jari lingkaran dan sudut pusat dinyatakan dalam radian.
• Menentukan panjang tali busur
  Panjang tali busur berbanding lurus dengan sinus sudut pusat. Sudut pusat yang lebih besar akan menghasilkan tali busur yang lebih panjang, dan sebaliknya.

Dengan demikian, sudut pusat merupakan aspek penting dari bagian lingkaran yang menentukan ukuran, bentuk, dan sifat-sifat bagian lingkaran.

Apotema

Apotema adalah garis yang menghubungkan titik pusat lingkaran dengan titik tengah tali busur. Dalam bagian lingkaran, apotema memiliki peran penting dalam menentukan sifat-sifat dan karakteristik bagian lingkaran.

• Menentukan tinggi bagian lingkaran
  Apotema tegak lurus terhadap tali busur dan membagi bagian lingkaran menjadi dua bagian yang sama besar. Panjang apotema menentukan tinggi bagian lingkaran, yaitu jarak antara tali busur dan titik tertinggi busur.
• Menghitung luas bagian lingkaran
  Luas bagian lingkaran dapat dihitung menggunakan rumus: Luas = (1/2) x panjang tali busur x apotema. Rumus ini menunjukkan bahwa luas bagian lingkaran berbanding lurus dengan panjang apotema.
• Menentukan panjang jari-jari lingkaran
  Dengan mengetahui panjang apotema dan tali busur, panjang jari-jari lingkaran dapat dihitung menggunakan rumus: jari-jari = (panjang tali busur² + 4 x apotema²) / 8 x apotema.
• Menghitung volume bangun ruang
  Apotema juga digunakan dalam menghitung volume bangun ruang yang melibatkan bagian lingkaran, seperti kerucut dan bola. Dalam kerucut, apotema digunakan untuk menghitung tinggi kerucut, sedangkan dalam bola, apotema digunakan untuk menghitung jari-jari bola.

Dengan demikian, apotema merupakan aspek penting dari bagian lingkaran yang berperan dalam menentukan sifat-sifat bagian lingkaran, menghitung luas dan volume bangun ruang, serta memiliki berbagai aplikasi dalam kehidupan nyata.

Tali busur

Tali busur adalah garis lurus yang menghubungkan dua titik pada lingkaran. Dalam bagian lingkaran, tali busur memiliki peran penting dan keterkaitan yang erat.

Salah satu peran penting tali busur adalah membagi bagian lingkaran menjadi dua bagian yang sama besar. Tali busur yang ditarik dari titik tengah busur akan membentuk garis simetri yang membagi bagian lingkaran menjadi dua bagian kongruen.

Selain itu, panjang tali busur juga menentukan besar sudut pusat yang terbentuk. Sudut pusat adalah sudut yang dibentuk oleh dua jari-jari yang ditarik dari titik pusat lingkaran ke titik-titik ujung tali busur. Semakin panjang tali busur, semakin besar sudut pusat yang terbentuk.

Dalam konteks kehidupan nyata, pemahaman tentang tali busur dan bagian lingkaran sangat penting dalam berbagai bidang, seperti:

• Arsitektur: Tali busur digunakan dalam merancang lengkungan, kubah, dan struktur melengkung lainnya.
• Teknik: Tali busur digunakan dalam mendesain jembatan, roda gigi, dan komponen mesin lainnya.
• Matematika: Tali busur digunakan dalam menghitung luas dan keliling bagian lingkaran, serta dalam trigonometri.

Dengan demikian, tali busur merupakan komponen penting dari bagian lingkaran yang memiliki peran penting dalam menentukan sifat-sifat bagian lingkaran dan memiliki berbagai aplikasi praktis dalam kehidupan sehari-hari.

Tangen

Dalam matematika, tangen adalah garis yang menyinggung lingkaran pada satu titik. Dalam konteks bagian lingkaran, tangen memiliki peran penting dan keterkaitan yang erat.

Salah satu peran penting tangen adalah menentukan titik singgung, yaitu titik di mana tangen menyinggung lingkaran. Titik singgung membagi bagian lingkaran menjadi dua bagian yang tidak tumpang tindih. Garis singgung yang ditarik dari titik luar lingkaran akan memotong lingkaran pada dua titik, yang membagi bagian lingkaran menjadi tiga bagian. Titik singgung dan pembagian bagian lingkaran ini penting dalam berbagai aplikasi, seperti:

• Konstruksi: Tangen digunakan dalam merancang kurva, lengkungan, dan permukaan melengkung lainnya.
• Trigonometri: Tangen digunakan dalam menghitung sudut dan jarak dalam segitiga siku-siku.
• Fisika: Tangen digunakan dalam menganalisis gerak benda yang bergerak melingkar.

Selain itu, kemiringan garis tangen pada titik singgung sama dengan gradien garis yang melalui titik pusat lingkaran dan titik singgung tersebut. Hal ini penting dalam kalkulus untuk menentukan turunan fungsi trigonometri dan persamaan garis singgung pada kurva.

Dengan demikian, tangen merupakan komponen penting dari bagian lingkaran yang memiliki peran penting dalam menentukan titik singgung, membagi bagian lingkaran, dan memiliki berbagai aplikasi praktis dalam berbagai bidang ilmu pengetahuan dan kehidupan sehari-hari.

Sekan

Sekan adalah garis yang memotong lingkaran pada dua titik. Dalam bagian lingkaran, sekan memiliki beberapa peran dan keterkaitan penting.

• Membagi bagian lingkaran menjadi beberapa bagian
  Sekan dapat digunakan untuk membagi bagian lingkaran menjadi beberapa bagian yang lebih kecil. Sekan yang melalui titik pusat lingkaran akan membagi bagian lingkaran menjadi dua bagian yang sama besar.
• Menentukan panjang tali busur
  Panjang tali busur sama dengan panjang sekan yang menghubungkan kedua ujung tali busur tersebut.
• Menghitung luas bagian lingkaran
  Luas bagian lingkaran dapat dihitung menggunakan rumus: Luas = (1/2) x (panjang sekan) x (apotema), di mana apotema adalah jarak dari tali busur ke titik pusat lingkaran.
• Menentukan sifat-sifat bagian lingkaran
  Sifat-sifat bagian lingkaran, seperti keliling dan luas, dapat dipengaruhi oleh panjang sekan yang digunakan untuk membentuk bagian lingkaran tersebut.

Dengan demikian, sekan merupakan komponen penting dari bagian lingkaran yang memiliki peran penting dalam menentukan sifat-sifat bagian lingkaran dan memiliki berbagai aplikasi dalam kehidupan sehari-hari.

Diameter

Diameter adalah garis lurus yang melalui titik pusat lingkaran dan menghubungkan dua titik pada lingkaran. Dalam konteks bagian lingkaran, diameter memiliki peran penting dan keterkaitan yang erat.

Diameter membagi lingkaran menjadi dua bagian yang sama besar, yaitu dua setengah lingkaran. Dalam bagian lingkaran, diameter menjadi batas dari bagian lingkaran tersebut. Panjang diameter sama dengan dua kali panjang jari-jari lingkaran, sehingga diameter merupakan faktor penting dalam menentukan ukuran bagian lingkaran.

Selain itu, diameter tegak lurus terhadap setiap tali busur yang menghubungkan dua titik pada lingkaran. Sifat ini digunakan dalam berbagai aplikasi, seperti dalam menentukan titik tengah lingkaran atau dalam konstruksi geometri.

Dalam kehidupan sehari-hari, pemahaman tentang diameter dan bagian lingkaran sangat penting dalam berbagai bidang, seperti:

• Arsitektur: Diameter digunakan dalam merancang lengkungan, kubah, dan struktur melengkung lainnya.
• Teknik: Diameter digunakan dalam mendesain roda, poros, dan komponen mesin lainnya.
• Matematika: Diameter digunakan dalam menghitung luas dan keliling lingkaran dan bagian lingkaran.

Dengan demikian, diameter merupakan komponen penting dari bagian lingkaran yang memiliki peran penting dalam menentukan sifat-sifat bagian lingkaran dan memiliki berbagai aplikasi praktis dalam kehidupan sehari-hari.

FAQ tentang “Bagian Lingkaran”

Berikut adalah beberapa pertanyaan umum dan jawabannya mengenai bagian lingkaran:

Pertanyaan 1: Apa yang dimaksud dengan bagian lingkaran?

Bagian lingkaran adalah bagian dari lingkaran yang dibatasi oleh dua jari-jari dan sebuah busur.

Pertanyaan 2: Apa saja jenis-jenis bagian lingkaran?

Jenis-jenis bagian lingkaran antara lain setengah lingkaran, seperempat lingkaran, dan bagian lingkaran lainnya.

Pertanyaan 3: Bagaimana cara menghitung luas bagian lingkaran?

Luas bagian lingkaran dapat dihitung menggunakan rumus: Luas = (r²/2) x sudut pusat, di mana r adalah jari-jari lingkaran dan sudut pusat dinyatakan dalam radian.

Pertanyaan 4: Apa saja aplikasi bagian lingkaran dalam kehidupan sehari-hari?

Bagian lingkaran memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti dalam arsitektur, teknik, dan matematika.

Pertanyaan 5: Bagaimana cara menggambar bagian lingkaran?

Bagian lingkaran dapat digambar menggunakan jangka dan penggaris, atau menggunakan perangkat lunak desain.

Pertanyaan 6: Apa itu apotema bagian lingkaran?

Apotema bagian lingkaran adalah garis yang menghubungkan titik pusat lingkaran dengan titik tengah tali busur.

Demikianlah beberapa pertanyaan umum dan jawabannya mengenai bagian lingkaran. Semoga informasi ini bermanfaat.

Kembali ke artikel utama

Tips Mengenai Bagian Lingkaran

Dengan memahami konsep dasar dan sifat-sifat bagian lingkaran, kita dapat memanfaatkannya secara efektif dalam berbagai bidang. Berikut adalah beberapa tips yang dapat membantu:

Tip 1: Manfaatkan sifat simetri

Bagian lingkaran memiliki sifat simetri, yang dapat dimanfaatkan untuk menyederhanakan perhitungan dan konstruksi. Misalnya, jika Anda ingin membagi bagian lingkaran menjadi dua bagian yang sama besar, cukup gambar garis yang melalui titik pusat dan titik tengah tali busur.

Tip 2: Gunakan rumus yang tepat

Ada beberapa rumus yang dapat digunakan untuk menghitung luas, keliling, dan sifat-sifat lainnya dari bagian lingkaran. Pastikan untuk menggunakan rumus yang tepat sesuai dengan jenis dan informasi yang tersedia.

Tip 3: Visualisasikan bagian lingkaran

Memvisualisasikan bagian lingkaran dapat membantu dalam memahami konsep dan sifat-sifatnya. Gunakan gambar atau diagram untuk merepresentasikan bagian lingkaran dan hubungan antara komponen-komponennya.

Tip 4: Latih soal-soal

Latihan soal adalah cara yang efektif untuk meningkatkan pemahaman dan keterampilan dalam menangani bagian lingkaran. Carilah soal-soal latihan yang beragam dan cobalah untuk menyelesaikannya tanpa bantuan.

Tip 5: Terapkan dalam kehidupan nyata

Bagian lingkaran memiliki banyak aplikasi dalam kehidupan nyata. Cobalah untuk mengidentifikasi situasi di mana Anda dapat menerapkan konsep bagian lingkaran, seperti dalam desain, arsitektur, atau teknik.

Kesimpulan

Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman dan kemampuan Anda dalam bekerja dengan bagian lingkaran. Ingatlah bahwa latihan dan eksplorasi yang berkelanjutan adalah kunci untuk menguasai konsep ini.

Kesimpulan

Bagian lingkaran merupakan konsep geometris penting yang memiliki peran krusial dalam berbagai bidang, seperti matematika, teknik, dan arsitektur. Pemahaman mendalam tentang bagian lingkaran sangat penting untuk menguasai konsep-konsep geometris yang lebih kompleks dan untuk memecahkan masalah di berbagai bidang kehidupan.

Dengan mengeksplorasi sifat-sifat, rumus, dan aplikasi bagian lingkaran, kita dapat memperoleh apresiasi yang lebih dalam tentang keindahan dan kegunaan matematika. Bagian lingkaran tidak hanya menjadi dasar bagi banyak penemuan ilmiah dan kemajuan teknologi, tetapi juga menjadi simbol harmoni dan kesatuan dalam dunia alam.

Youtube Video: