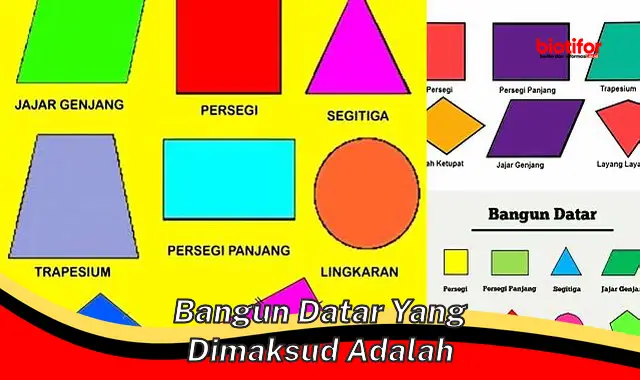
Bangun datar yang dimaksud adalah sebuah istilah dalam matematika yang merujuk pada suatu bangun dua dimensi yang memiliki sisi dan sudut yang jelas. Istilah ini umum digunakan dalam geometri untuk menggambarkan bentuk-bentuk seperti persegi, segitiga, lingkaran, dan jajaran genjang. Bangun datar merupakan salah satu konsep dasar dalam matematika yang dipelajari mulai dari tingkat sekolah dasar.
Dalam kehidupan sehari-hari, bangun datar memiliki peran penting dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Arsitek menggunakan bangun datar untuk merancang bangunan dan menentukan ukuran ruangan. Insinyur menggunakannya untuk menghitung kekuatan dan stabilitas struktur, sedangkan desainer menggunakannya untuk menciptakan berbagai macam bentuk dan pola.
Mempelajari bangun datar sangat bermanfaat untuk mengembangkan keterampilan berpikir logis dan spasial. Siswa yang memahami konsep bangun datar akan lebih mudah memahami materi matematika yang lebih kompleks, seperti trigonometri dan kalkulus. Selain itu, pemahaman tentang bangun datar juga dapat membantu kita dalam kehidupan sehari-hari, seperti saat kita mengukur luas tanah atau menghitung volume sebuah benda.
bangun datar yang dimaksud adalah
Bangun datar yang dimaksud adalah merupakan sebuah konsep penting dalam matematika, khususnya geometri. Konsep ini mengacu pada bentuk-bentuk dua dimensi yang memiliki sisi dan sudut yang jelas. Dalam kehidupan sehari-hari, bangun datar memiliki banyak aplikasi, seperti dalam arsitektur, teknik, dan desain.
- Definisi
- Jenis-jenis
- Sifat-sifat
- Luas dan keliling
- Aplikasi
- Sejarah
- Tokoh-tokoh penting
- Contoh
- Perkembangan
Dengan memahami berbagai aspek tersebut, kita dapat memperoleh pemahaman yang lebih komprehensif tentang bangun datar yang dimaksud adalah. Konsep ini tidak hanya penting dalam matematika, tetapi juga memiliki banyak aplikasi dalam kehidupan nyata. Misalnya, dalam arsitektur, bangun datar digunakan untuk merancang bangunan dan menentukan ukuran ruangan. Dalam teknik, bangun datar digunakan untuk menghitung kekuatan dan stabilitas struktur. Dalam desain, bangun datar digunakan untuk menciptakan berbagai macam bentuk dan pola.
Definisi
Definisi merupakan aspek krusial dalam memahami konsep bangun datar yang dimaksud adalah. Definisi yang jelas dan komprehensif memberikan landasan untuk eksplorasi lebih lanjut tentang sifat-sifat, jenis-jenis, dan aplikasi bangun datar.
-
Konsep Geometris
Dalam geometri, bangun datar didefinisikan sebagai bentuk dua dimensi yang memiliki batas yang jelas, berupa sisi dan sudut. Definisi ini membedakan bangun datar dari bangun ruang yang memiliki tiga dimensi.
-
Unsur-unsur Bangun Datar
Definisi bangun datar juga mencakup unsur-unsurnya, yaitu sisi, sudut, diagonal, dan simetri. Unsur-unsur ini menjadi dasar untuk mengklasifikasikan dan membandingkan berbagai jenis bangun datar.
-
Sifat-sifat Bangun Datar
Definisi yang komprehensif juga menjelaskan sifat-sifat umum bangun datar, seperti kekongruenan, kesebangunan, dan simetri. Sifat-sifat ini memberikan wawasan tentang hubungan dan pola antarbangun datar.
-
Jenis-jenis Bangun Datar
Berdasarkan definisinya, bangun datar dapat diklasifikasikan menjadi berbagai jenis, seperti segitiga, persegi, lingkaran, dan trapesium. Setiap jenis bangun datar memiliki karakteristik dan sifat unik yang membedakannya dari jenis lainnya.
Dengan memahami definisi bangun datar yang dimaksud adalah secara jelas, kita dapat membangun pemahaman yang kuat tentang konsep ini dan berbagai aspeknya. Definisi tersebut berfungsi sebagai titik awal untuk eksplorasi lebih lanjut, membuka jalan bagi pembahasan tentang sifat-sifat, jenis-jenis, aplikasi, dan peran penting bangun datar dalam berbagai bidang.
Jenis-jenis
Konsep jenis-jenis bangun datar yang dimaksud adalah merupakan aspek penting dalam memahami keragaman bentuk dan sifat bangun datar. Berbagai jenis bangun datar memiliki karakteristik unik yang membedakannya satu sama lain, sehingga penting untuk mengeksplorasi jenis-jenis ini secara mendalam.
-
Segitiga
Segitiga adalah bangun datar yang memiliki tiga sisi dan tiga sudut. Segitiga memiliki berbagai jenis, seperti segitiga siku-siku, segitiga sama sisi, dan segitiga sama kaki.
-
Segiempat
Segiempat adalah bangun datar yang memiliki empat sisi dan empat sudut. Segiempat memiliki berbagai jenis, seperti persegi, persegi panjang, jajaran genjang, dan trapesium.
-
Lingkaran
Lingkaran adalah bangun datar yang dibatasi oleh kurva tertutup yang disebut keliling. Lingkaran memiliki sifat unik, seperti tidak memiliki sisi dan sudut.
-
Jajar Genjang
Jajar genjang adalah bangun datar yang memiliki dua pasang sisi sejajar. Jajar genjang memiliki sifat khusus, seperti memiliki luas yang sama dengan luas persegi panjang yang memiliki alas dan tinggi yang sama dengan jajar genjang tersebut.
Dengan memahami berbagai jenis bangun datar yang dimaksud adalah, kita dapat memperoleh pemahaman yang lebih komprehensif tentang konsep bangun datar secara keseluruhan. Jenis-jenis bangun datar ini menjadi dasar untuk mempelajari sifat-sifat, luas, keliling, dan aplikasi bangun datar dalam berbagai bidang.
Sifat-sifat
Sifat-sifat merupakan karakteristik yang membedakan satu bangun datar yang dimaksud adalah dengan bangun datar lainnya. Sifat-sifat ini menentukan bentuk, ukuran, dan perilaku bangun datar dalam berbagai operasi geometri.
-
Kesebangunan
Kesebangunan adalah sifat dua bangun datar yang memiliki bentuk yang sama tetapi tidak harus memiliki ukuran yang sama. Bangun datar yang sebangun memiliki sudut-sudut yang sama besar dan sisi-sisi yang sebanding.
-
Kekongruenan
Kekongruenan adalah sifat dua bangun datar yang memiliki bentuk dan ukuran yang sama. Bangun datar yang kongruen memiliki sudut-sudut yang sama besar dan sisi-sisi yang sama panjang.
-
Simetri
Simetri adalah sifat suatu bangun datar yang memiliki kesamaan bentuk pada kedua sisinya. Bangun datar dapat memiliki simetri lipat, simetri putar, atau kombinasi keduanya.
-
Luas dan Keliling
Luas dan keliling adalah sifat bangun datar yang berkaitan dengan ukurannya. Luas suatu bangun datar adalah ukuran permukaannya, sedangkan keliling suatu bangun datar adalah panjang batas luarnya.
Dengan memahami sifat-sifat bangun datar yang dimaksud adalah, kita dapat mengklasifikasikan, membandingkan, dan menganalisis berbagai bangun datar. Sifat-sifat ini juga menjadi dasar untuk menghitung luas dan keliling bangun datar, yang sangat penting dalam berbagai aplikasi praktis, seperti arsitektur, teknik, dan desain.
Luas dan keliling
Luas dan keliling merupakan dua sifat penting yang terkait erat dengan bangun datar yang dimaksud adalah. Luas suatu bangun datar menyatakan ukuran permukaannya, sedangkan keliling suatu bangun datar menyatakan panjang batas luarnya. Kedua sifat ini memiliki peran penting dalam berbagai aplikasi praktis, seperti arsitektur, teknik, dan desain.
-
Mengukur Luas Bangun Datar
Luas bangun datar digunakan untuk mengukur ukuran permukaan suatu bidang. Dalam arsitektur, luas lantai digunakan untuk menentukan ukuran ruangan dan menghitung kebutuhan material. Dalam teknik, luas permukaan benda digunakan untuk menghitung gaya hambat dan perpindahan panas.
-
Menghitung Keliling Bangun Datar
Keliling bangun datar digunakan untuk mengukur panjang batas luar suatu bidang. Dalam teknik, keliling roda digunakan untuk menghitung jarak yang ditempuh oleh kendaraan. Dalam desain, keliling suatu objek digunakan untuk menentukan ukuran bingkai atau pembatas.
-
Relasi Luas dan Keliling
Dalam beberapa kasus, terdapat hubungan antara luas dan keliling bangun datar. Misalnya, untuk bangun datar yang sebangun, rasio luas terhadap kuadrat kelilingnya adalah konstan. Hubungan ini digunakan dalam berbagai aplikasi, seperti optimasi bentuk dan desain struktural.
-
Aplikasi dalam Kehidupan Sehari-hari
Luas dan keliling bangun datar memiliki banyak aplikasi dalam kehidupan sehari-hari. Misalnya, luas tanah digunakan untuk menghitung pajak bumi dan bangunan. Keliling pagar digunakan untuk menentukan jumlah bahan yang dibutuhkan untuk membangun pagar.
Dengan memahami konsep luas dan keliling bangun datar yang dimaksud adalah, kita dapat menyelesaikan berbagai masalah praktis dan membuat keputusan yang tepat dalam berbagai bidang. Kedua sifat ini merupakan bagian penting dari geometri dan memiliki peran penting dalam kehidupan kita sehari-hari.
Aplikasi
Aplikasi merupakan salah satu aspek penting dalam memahami bangun datar yang dimaksud adalah. Bangun datar memiliki banyak aplikasi dalam berbagai bidang kehidupan, seperti arsitektur, teknik, desain, dan sains. Memahami aplikasi bangun datar sangat penting untuk mengaplikasikan konsep matematika dalam kehidupan nyata.
Dalam arsitektur, bangun datar digunakan untuk merancang denah bangunan, menghitung luas ruangan, dan menentukan kebutuhan material. Dalam teknik, bangun datar digunakan untuk menghitung kekuatan dan stabilitas struktur, serta merancang mesin dan peralatan. Dalam desain, bangun datar digunakan untuk menciptakan berbagai macam bentuk dan pola, baik untuk produk industri maupun karya seni.
Salah satu aplikasi penting bangun datar adalah dalam bidang sains. Dalam fisika, bangun datar digunakan untuk menghitung luas permukaan dan volume benda, yang sangat penting dalam bidang seperti mekanika fluida dan termodinamika. Dalam biologi, bangun datar digunakan untuk menganalisis bentuk dan struktur organisme, serta untuk memodelkan penyebaran penyakit dan pertumbuhan populasi.
Dengan memahami aplikasi bangun datar yang dimaksud adalah, kita dapat melihat keterkaitan antara matematika dan dunia nyata. Konsep bangun datar tidak hanya penting dalam teori matematika, tetapi juga memiliki peran penting dalam berbagai bidang praktis. Memahami aplikasi bangun datar dapat membantu kita memecahkan masalah, membuat keputusan, dan memahami dunia di sekitar kita.
Sejarah
Sejarah memainkan peran penting dalam perkembangan konsep bangun datar yang dimaksud adalah. Sejak zaman dahulu, manusia telah menggunakan bangun datar untuk memecahkan masalah praktis dan memahami dunia di sekitar mereka.
-
Awal Mula Geometri
Konsep bangun datar berawal dari peradaban Mesir dan Babilonia kuno. Bangsa Mesir menggunakan geometri untuk mengukur tanah dan membangun piramida, sedangkan bangsa Babilonia mengembangkan sistem bilangan berbasis 60 yang digunakan dalam pengukuran sudut dan jarak.
-
Geometri Yunani
Matematikawan Yunani seperti Thales, Pythagoras, dan Euclid memberikan kontribusi signifikan terhadap perkembangan geometri. Mereka mengembangkan teorema dan aksioma yang menjadi dasar geometri hingga saat ini, termasuk teorema Pythagoras dan postulat Euclid.
-
Geometri Modern
Pada abad ke-19 dan ke-20, matematikawan seperti Bernhard Riemann dan Georg Cantor mengembangkan konsep geometri baru, seperti geometri non-Euclid dan teori himpunan. Konsep-konsep ini memperluas pemahaman kita tentang bangun datar dan hubungannya dengan ruang dan waktu.
-
Geometri Komputer
Dalam beberapa dekade terakhir, perkembangan komputer telah merevolusi cara kita mempelajari dan menerapkan geometri. Grafik komputer dan perangkat lunak desain telah membuat visualisasi dan manipulasi bangun datar menjadi lebih mudah, sehingga memperluas jangkauan aplikasi geometri di berbagai bidang.
Dengan memahami sejarah bangun datar yang dimaksud adalah, kita dapat menghargai kontribusi para matematikawan dan ilmuwan sepanjang sejarah. Sejarah ini juga memberikan konteks untuk memahami perkembangan konsep geometri dan aplikasinya yang luas dalam kehidupan modern.
Tokoh-tokoh Penting
Dalam sejarah perkembangan bangun datar yang dimaksud adalah, terdapat beberapa tokoh penting yang memberikan kontribusi signifikan. Tokoh-tokoh ini mengembangkan konsep, teorema, dan metode yang menjadi landasan geometri modern dan memiliki pengaruh besar pada pemahaman kita tentang bangun datar.
Salah satu tokoh paling terkenal dalam geometri adalah Euclid, seorang matematikawan Yunani yang hidup pada abad ke-3 SM. Euclid menulis buku “Elemen”, yang berisi kumpulan aksioma, postulat, dan teorema yang menjadi dasar geometri hingga saat ini. “Elemen” menjadi salah satu buku teks matematika yang paling berpengaruh sepanjang sejarah dan masih dipelajari oleh siswa di seluruh dunia.
Tokoh penting lainnya dalam geometri adalah Pythagoras, seorang filsuf dan matematikawan Yunani yang hidup pada abad ke-6 SM. Pythagoras terkenal dengan teoremanya yang terkenal, yang menyatakan bahwa dalam sebuah segitiga siku-siku, kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang kedua sisi lainnya. Teorema Pythagoras memiliki banyak aplikasi dalam bidang matematika dan sains, termasuk trigonometri, fisika, dan teknik.
Selain Euclid dan Pythagoras, ada banyak tokoh penting lainnya yang berkontribusi pada perkembangan geometri dan konsep bangun datar. Tokoh-tokoh ini mencakup Archimedes, Ren Descartes, Carl Friedrich Gauss, dan Bernhard Riemann. Kontribusi mereka telah memperluas pemahaman kita tentang bangun datar dan membuka jalan bagi aplikasi baru dalam berbagai bidang.
Contoh
Contoh memainkan peran penting dalam memahami “bangun datar yang dimaksud adalah”. Contoh membantu mengilustrasikan konsep abstrak dan menunjukkan bagaimana bangun datar diterapkan dalam kehidupan nyata.
Misalnya, ketika mempelajari konsep segitiga, siswa mungkin diberikan contoh segitiga siku-siku, segitiga sama sisi, dan segitiga sama kaki. Contoh-contoh ini membantu siswa memahami sifat dan karakteristik yang berbeda dari berbagai jenis segitiga.
Demikian pula, ketika mempelajari konsep luas dan keliling bangun datar, siswa mungkin diberikan contoh cara menghitung luas persegi panjang, segitiga, dan lingkaran. Contoh-contoh ini membantu siswa memahami cara menerapkan rumus dan konsep untuk memecahkan masalah praktis.
Memahami hubungan antara “Contoh” dan “bangun datar yang dimaksud adalah” sangat penting karena beberapa alasan:
- Contoh membantu membuat konsep abstrak menjadi nyata dan mudah dipahami.
- Contoh menunjukkan bagaimana bangun datar digunakan dalam kehidupan sehari-hari, sehingga memperkuat pembelajaran.
- Contoh memberikan kesempatan bagi siswa untuk berlatih menerapkan konsep dan keterampilan, sehingga meningkatkan pemahaman.
Perkembangan
Perkembangan merupakan aspek penting dalam memahami “bangun datar yang dimaksud adalah”. Perkembangan mencakup kemajuan dan inovasi konseptual, teoretis, dan praktis yang memperkaya pemahaman kita tentang bangun datar.
-
Perkembangan Konseptual
Perkembangan konseptual mengacu pada perluasan dan pendalaman konsep bangun datar. Seiring waktu, matematikawan dan ilmuwan telah mengembangkan konsep baru seperti geometri non-Euclid, dimensi fraksional, dan topologi, yang memperluas pemahaman kita tentang bentuk dan ruang.
-
Perkembangan Teoretis
Perkembangan teoretis melibatkan penemuan teorema, aksioma, dan prinsip baru yang menjelaskan sifat dan perilaku bangun datar. Misalnya, pengembangan teorema Euler tentang polihedron dan teorema Four Color tentang pewarnaan peta merupakan tonggak penting dalam perkembangan geometri.
-
Perkembangan Praktis
Perkembangan praktis mengacu pada penerapan konsep dan teori bangun datar dalam berbagai bidang. Misalnya, geometri digunakan dalam arsitektur untuk merancang struktur, dalam teknik untuk menganalisis kekuatan dan stabilitas, dan dalam komputer untuk mengembangkan grafik dan algoritma.
-
Perkembangan Teknologi
Perkembangan teknologi, seperti komputer dan perangkat lunak desain, telah merevolusi cara kita mempelajari dan menerapkan geometri. Visualisasi dan manipulasi bangun datar menjadi lebih mudah, memungkinkan kita untuk mengeksplorasi konsep yang kompleks dan memecahkan masalah dengan cara yang baru.
Dengan memahami perkembangan “bangun datar yang dimaksud adalah”, kita dapat melihat bagaimana konsep ini terus berkembang dan diterapkan dalam berbagai bidang. Perkembangan ini tidak hanya memperkaya pemahaman kita tentang matematika, tetapi juga memberikan alat yang ampuh untuk kemajuan ilmiah dan teknologi.
Tanya Jawab tentang Bangun Datar yang Dimaksud Adalah
Untuk memberikan pemahaman yang komprehensif, berikut adalah beberapa pertanyaan umum dan jawabannya terkait dengan “bangun datar yang dimaksud adalah”.
Pertanyaan 1: Apa yang dimaksud dengan bangun datar?
Jawaban: Bangun datar adalah sebuah bentuk dua dimensi yang memiliki batas yang jelas, berupa sisi dan sudut.
Pertanyaan 2: Apa saja jenis-jenis bangun datar?
Jawaban: Jenis-jenis bangun datar meliputi segitiga, persegi, lingkaran, jajaran genjang, dan trapesium.
Pertanyaan 3: Apa saja sifat-sifat bangun datar?
Jawaban: Sifat-sifat bangun datar meliputi kesebangunan, kekongruenan, simetri, luas, dan keliling.
Pertanyaan 4: Bagaimana cara menghitung luas bangun datar?
Jawaban: Luas bangun datar dapat dihitung menggunakan rumus yang berbeda-beda, tergantung jenis bangun datar tersebut.
Pertanyaan 5: Bagaimana cara menghitung keliling bangun datar?
Jawaban: Keliling bangun datar dapat dihitung menggunakan rumus yang berbeda-beda, tergantung jenis bangun datar tersebut.
Pertanyaan 6: Apa saja aplikasi bangun datar dalam kehidupan sehari-hari?
Jawaban: Bangun datar memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti dalam arsitektur, teknik, dan desain.
Dengan memahami jawaban-jawaban di atas, kita dapat memperoleh pemahaman yang baik tentang “bangun datar yang dimaksud adalah”. Konsep ini sangat penting dalam matematika dan memiliki banyak aplikasi dalam berbagai bidang kehidupan.
Transisi ke bagian artikel selanjutnya:
Untuk mempelajari lebih lanjut tentang bangun datar yang dimaksud adalah, silakan lanjutkan membaca bagian selanjutnya dari artikel ini.
Tips Memahami Bangun Datar yang Dimaksud Adalah
Untuk memahami konsep bangun datar dengan baik, berikut adalah beberapa tips yang dapat membantu:
Tip 1: Pahami Definisi dan Jenis-jenisnya
Mulailah dengan memahami definisi bangun datar dan berbagai jenisnya, seperti segitiga, persegi, lingkaran, dan lainnya. Ini akan memberikan dasar untuk mempelajari sifat dan aplikasinya.
Tip 2: Kuasai Sifat-sifatnya
Sifat-sifat bangun datar, seperti kesebangunan, kekongruenan, dan simetri, sangat penting untuk dipahami. Sifat-sifat ini menentukan bentuk, ukuran, dan perilaku bangun datar.
Tip 3: Latih Menghitung Luas dan Keliling
Luas dan keliling merupakan aspek penting dalam memahami bangun datar. Berlatihlah menghitung luas dan keliling menggunakan rumus yang berbeda untuk setiap jenis bangun datar.
Tip 4: Carilah Contoh dan Aplikasi dalam Kehidupan Nyata
Bangun datar memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti dalam arsitektur, teknik, dan desain. Carilah contoh dan terapkan konsep bangun datar ke dalam situasi nyata.
Tip 5: Manfaatkan Sumber Belajar yang Tersedia
Ada banyak sumber belajar yang tersedia, seperti buku teks, video tutorial, dan situs web. Manfaatkan sumber-sumber ini untuk memperkuat pemahaman dan memperoleh informasi tambahan.
Tip 6: Diskusikan dengan Guru atau Teman
Diskusikan konsep dan masalah bangun datar dengan guru atau teman. Bertukar pikiran dan memberikan penjelasan dapat meningkatkan pemahaman.
Tip 7: Jangan Takut Bertanya
Jika ada konsep yang tidak dipahami, jangan ragu untuk bertanya kepada guru, teman, atau sumber belajar lainnya. Bertanya akan membantu mengatasi kesulitan dan meningkatkan pemahaman.
Tip 8: Bersabar dan Konsisten
Memahami bangun datar membutuhkan waktu dan latihan yang konsisten. Bersabarlah dalam proses pembelajaran dan teruslah berlatih untuk meningkatkan pemahaman.
Dengan mengikuti tips-tips ini, Anda dapat meningkatkan pemahaman tentang bangun datar yang dimaksud adalah dan mengaplikasikan konsepnya dalam berbagai bidang.
Transisi ke bagian kesimpulan artikel:
Dengan memahami bangun datar yang dimaksud adalah, kita dapat memperoleh keterampilan penting dalam matematika dan mengembangkan kemampuan berpikir logis dan spasial.
Kesimpulan
Dengan memahami “bangun datar yang dimaksud adalah”, kita memperoleh pemahaman yang komprehensif tentang konsep dasar dalam matematika. Bangun datar memiliki berbagai jenis, sifat, dan aplikasi dalam kehidupan sehari-hari, seperti dalam arsitektur, teknik, dan desain.
Memahami bangun datar tidak hanya mengembangkan keterampilan matematika, tetapi juga kemampuan berpikir logis dan spasial. Konsep ini merupakan dasar untuk memahami konsep matematika yang lebih kompleks dan memecahkan masalah di berbagai bidang. Dengan terus belajar dan mengeksplorasi konsep bangun datar, kita dapat memperoleh pemahaman yang lebih dalam tentang dunia di sekitar kita.
Youtube Video:
