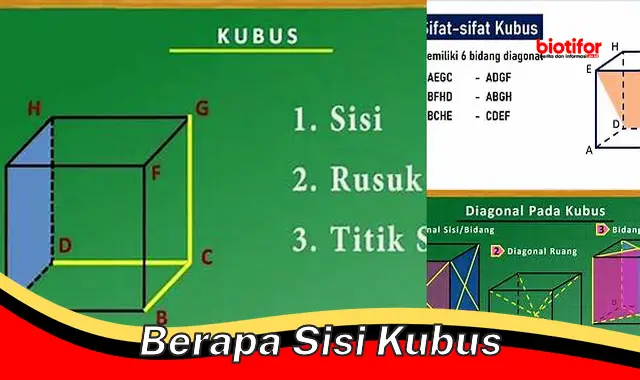
Berapa sisi kubus adalah pertanyaan yang sering diajukan dalam matematika. Kubus adalah bangun ruang tiga dimensi yang memiliki enam sisi berbentuk persegi. Sisi-sisi tersebut sama ukuran dan saling tegak lurus. Kubus juga memiliki 12 rusuk dan 8 titik sudut.
Mengetahui berapa sisi kubus penting dalam matematika karena kubus merupakan salah satu bangun ruang dasar yang banyak digunakan dalam berbagai bidang, seperti geometri, fisika, dan teknik. Pemahaman tentang kubus juga membantu kita memahami konsep volume dan luas permukaan bangun ruang tiga dimensi.
Dalam kehidupan sehari-hari, kita dapat menemukan banyak contoh kubus, seperti dadu, kotak kardus, dan akuarium. Memahami sifat-sifat kubus dapat membantu kita memecahkan masalah dan membuat keputusan yang tepat dalam kehidupan sehari-hari.
Berapa Sisi Kubus
Memahami berapa sisi kubus sangat penting dalam matematika dan kehidupan sehari-hari. Berikut adalah 9 aspek penting terkait “berapa sisi kubus”:
- Bangun ruang tiga dimensi
- Enam sisi berbentuk persegi
- Sisi sama ukuran
- Sisi saling tegak lurus
- 12 rusuk
- 8 titik sudut
- Konsep volume
- Konsep luas permukaan
- Contoh dalam kehidupan sehari-hari (dadu, kotak kardus, akuarium)
Memahami aspek-aspek ini membantu kita memahami sifat-sifat kubus, menghitung volumenya, dan menyelesaikan masalah terkait kubus. Misalnya, mengetahui bahwa kubus memiliki enam sisi berbentuk persegi membantu kita menghitung luas permukaannya. Memahami konsep volume kubus membantu kita menentukan kapasitas wadah berbentuk kubus, seperti akuarium atau kotak kardus.
Bangun Ruang Tiga Dimensi
Dalam matematika, bangun ruang tiga dimensi adalah bangun yang memiliki panjang, lebar, dan tinggi. Kubus adalah salah satu contoh bangun ruang tiga dimensi. Kubus memiliki enam sisi berbentuk persegi yang sama ukuran dan saling tegak lurus. Dengan memahami konsep bangun ruang tiga dimensi, kita dapat memahami sifat-sifat kubus, termasuk berapa sisi yang dimilikinya.
Memahami hubungan antara bangun ruang tiga dimensi dan berapa sisi kubus sangat penting karena:
- Membantu kita menghitung volume dan luas permukaan kubus.
- Membantu kita memahami sifat-sifat kubus dan bangun ruang tiga dimensi lainnya.
- Membantu kita memecahkan masalah yang melibatkan kubus dan bangun ruang tiga dimensi lainnya.
Dalam kehidupan sehari-hari, kita dapat menemukan banyak contoh bangun ruang tiga dimensi, seperti kotak kardus, akuarium, dan dadu. Memahami konsep bangun ruang tiga dimensi dan berapa sisi kubus dapat membantu kita memahami sifat-sifat benda-benda tersebut dan menyelesaikan masalah yang melibatkan benda-benda tersebut.
Enam Sisi Berbentuk Persegi
Dalam geometri, kubus adalah bangun ruang tiga dimensi yang memiliki enam sisi berbentuk persegi. Hubungan antara “enam sisi berbentuk persegi” dan “berapa sisi kubus” sangat penting untuk memahami sifat-sifat kubus dan menyelesaikan masalah yang melibatkan kubus.
-
Sisi yang Sama Ukuran
Kubus memiliki enam sisi berbentuk persegi yang sama ukuran. Artinya, keempat sisi kubus memiliki panjang yang sama. Sifat ini penting untuk menghitung luas permukaan dan volume kubus.
-
Sisi yang Saling Tegak Lurus
Keenam sisi kubus saling tegak lurus. Artinya, jika kita mengambil dua sisi kubus yang berdekatan, maka kedua sisi tersebut akan membentuk sudut 90 derajat. Sifat ini penting untuk menghitung volume dan luas permukaan kubus.
-
Membentuk Sudut Ruang
Keenam sisi kubus membentuk delapan sudut ruang. Sudut ruang adalah titik di mana tiga sisi kubus bertemu. Sifat ini penting untuk memahami sifat-sifat kubus dan menyelesaikan masalah yang melibatkan kubus.
-
Contoh dalam Kehidupan Sehari-hari
Banyak benda dalam kehidupan sehari-hari yang memiliki enam sisi berbentuk persegi, seperti dadu, kotak kardus, dan akuarium. Memahami sifat-sifat kubus dan hubungannya dengan “enam sisi berbentuk persegi” dapat membantu kita memahami sifat-sifat benda-benda tersebut dan menyelesaikan masalah yang melibatkan benda-benda tersebut.
Dengan memahami hubungan antara “enam sisi berbentuk persegi” dan “berapa sisi kubus”, kita dapat memahami sifat-sifat kubus, menghitung volumenya, dan menyelesaikan masalah yang melibatkan kubus. Sifat-sifat ini juga dapat diterapkan untuk memahami sifat-sifat benda-benda lain yang memiliki enam sisi berbentuk persegi.
Sisi sama ukuran
Dalam geometri, kubus adalah bangun ruang tiga dimensi yang memiliki enam sisi berbentuk persegi yang sama ukuran. Hubungan antara “sisi sama ukuran” dan “berapa sisi kubus” sangat penting untuk memahami sifat-sifat kubus dan menyelesaikan masalah yang melibatkan kubus.
Sifat “sisi sama ukuran” pada kubus memiliki beberapa implikasi penting:
-
Menentukan Volume dan Luas Permukaan
Karena sisi-sisi kubus sama ukuran, kita dapat dengan mudah menghitung volume dan luas permukaan kubus menggunakan rumus yang sederhana. Volume kubus sama dengan sisi dan luas permukaan kubus sama dengan 6 sisi. Sifat ini sangat penting dalam berbagai aplikasi, seperti arsitektur dan teknik. -
Membentuk Simetri
Sisi-sisi kubus yang sama ukuran menghasilkan simetri pada kubus. Kubus memiliki sembilan bidang simetri dan tiga sumbu simetri. Sifat simetri ini penting dalam kristalografi dan bidang lainnya. -
Contoh dalam Kehidupan Nyata
Banyak benda dalam kehidupan nyata yang memiliki sisi-sisi sama ukuran, seperti dadu, kotak kardus, dan kontainer penyimpanan. Memahami sifat “sisi sama ukuran” pada kubus dapat membantu kita memahami sifat benda-benda tersebut dan memecahkan masalah yang melibatkan benda-benda tersebut.
Dengan memahami hubungan antara “sisi sama ukuran” dan “berapa sisi kubus”, kita dapat memahami sifat-sifat kubus, menghitung volumenya, dan menyelesaikan masalah yang melibatkan kubus. Sifat-sifat ini juga dapat diterapkan untuk memahami sifat-sifat benda-benda lain yang memiliki sisi-sisi sama ukuran.
Sisi Saling Tegak Lurus
Dalam geometri, kubus adalah bangun ruang tiga dimensi yang memiliki sifat unik, yaitu keenam sisinya saling tegak lurus. Hubungan antara “sisi saling tegak lurus” dan “berapa sisi kubus” sangat penting untuk memahami sifat-sifat kubus dan menyelesaikan masalah yang melibatkan kubus.
-
Sudut 90 Derajat
Sisi-sisi kubus saling tegak lurus, artinya jika kita mengambil dua sisi kubus yang berdekatan, maka kedua sisi tersebut akan membentuk sudut 90 derajat. Sifat ini sangat penting dalam menghitung volume dan luas permukaan kubus, serta dalam menentukan sifat-sifat simetri kubus. -
Simetri Kubus
Sisi-sisi kubus yang saling tegak lurus menghasilkan sifat simetri yang tinggi pada kubus. Kubus memiliki sembilan bidang simetri dan tiga sumbu simetri. Sifat simetri ini penting dalam berbagai bidang, seperti kristalografi dan arsitektur. -
Contoh dalam Kehidupan Nyata
Banyak benda dalam kehidupan nyata yang memiliki sisi-sisi yang saling tegak lurus, seperti kotak kardus, lemari, dan gedung. Memahami hubungan antara “sisi saling tegak lurus” dan “berapa sisi kubus” dapat membantu kita memahami sifat benda-benda tersebut dan menyelesaikan masalah yang melibatkan benda-benda tersebut.
Dengan memahami hubungan antara “sisi saling tegak lurus” dan “berapa sisi kubus”, kita dapat memahami sifat-sifat kubus, menghitung volumenya, dan menyelesaikan masalah yang melibatkan kubus. Sifat-sifat ini juga dapat diterapkan untuk memahami sifat-sifat benda-benda lain yang memiliki sisi-sisi yang saling tegak lurus.
12 Rusuk
Dalam geometri, kubus adalah bangun ruang tiga dimensi yang memiliki 12 rusuk. Rusuk adalah garis yang menghubungkan dua titik sudut pada kubus. Setiap rusuk kubus memiliki panjang yang sama. Hubungan antara “12 rusuk” dan “berapa sisi kubus” sangat penting untuk memahami sifat-sifat kubus dan menyelesaikan masalah yang melibatkan kubus.
Jumlah rusuk pada kubus dapat ditentukan dengan rumus E = s x 12, di mana E adalah jumlah rusuk dan s adalah panjang sisi kubus. Rumus ini dapat digunakan untuk menghitung jumlah rusuk kubus dengan cepat dan mudah. Memahami hubungan antara “12 rusuk” dan “berapa sisi kubus” juga dapat membantu kita memahami sifat-sifat kubus lainnya, seperti luas permukaan dan volume.
Dalam kehidupan nyata, kita dapat menemukan banyak benda yang memiliki 12 rusuk, seperti dadu, kotak kardus, dan akuarium. Memahami hubungan antara “12 rusuk” dan “berapa sisi kubus” dapat membantu kita memahami sifat benda-benda tersebut dan menyelesaikan masalah yang melibatkan benda-benda tersebut. Misalnya, kita dapat menggunakan rumus E = s x 12 untuk menghitung jumlah rusuk pada sebuah kotak kardus atau akuarium.
8 titik sudut
Dalam geometri, kubus adalah bangun ruang tiga dimensi yang memiliki 8 titik sudut. Titik sudut adalah titik di mana tiga sisi kubus bertemu. Hubungan antara “8 titik sudut” dan “berapa sisi kubus” sangat penting untuk memahami sifat-sifat kubus dan menyelesaikan masalah yang melibatkan kubus.
Jumlah titik sudut pada kubus dapat ditentukan dengan rumus V = 8, di mana V adalah jumlah titik sudut. Rumus ini dapat digunakan untuk menghitung jumlah titik sudut kubus dengan cepat dan mudah. Memahami hubungan antara “8 titik sudut” dan “berapa sisi kubus” juga dapat membantu kita memahami sifat-sifat kubus lainnya, seperti luas permukaan dan volume.
Dalam kehidupan nyata, kita dapat menemukan banyak benda yang memiliki 8 titik sudut, seperti dadu, kotak kardus, dan akuarium. Memahami hubungan antara “8 titik sudut” dan “berapa sisi kubus” dapat membantu kita memahami sifat benda-benda tersebut dan menyelesaikan masalah yang melibatkan benda-benda tersebut. Misalnya, kita dapat menggunakan rumus V = 8 untuk menghitung jumlah titik sudut pada sebuah kotak kardus atau akuarium.
Konsep Volume
Dalam geometri, konsep volume sangat terkait dengan “berapa sisi kubus”. Volume suatu bangun ruang adalah ukuran ruang tiga dimensi yang ditempati oleh bangun ruang tersebut. Dalam hal kubus, volume dapat dihitung dengan rumus V = s, di mana s adalah panjang sisi kubus.
Memahami konsep volume kubus sangat penting karena memungkinkan kita untuk menentukan kapasitas atau ruang yang dapat ditampung oleh kubus. Misalnya, jika kita memiliki sebuah akuarium berbentuk kubus, kita dapat menggunakan konsep volume untuk menentukan jumlah air yang dapat ditampung oleh akuarium tersebut. Konsep volume juga penting dalam berbagai bidang, seperti arsitektur, teknik, dan logistik.
Selain itu, konsep volume juga terkait dengan sifat-sifat kubus lainnya, seperti luas permukaan dan jumlah rusuk. Dengan memahami hubungan antara konsep volume dan berapa sisi kubus, kita dapat lebih memahami sifat-sifat kubus secara keseluruhan dan menyelesaikan masalah yang melibatkan kubus.
Konsep Luas Permukaan
Konsep luas permukaan sangat terkait dengan “berapa sisi kubus”. Luas permukaan suatu bangun ruang adalah ukuran luas seluruh permukaan bangun ruang tersebut. Dalam hal kubus, luas permukaan dapat dihitung dengan rumus L = 6s, di mana s adalah panjang sisi kubus.
-
Menentukan Ukuran Permukaan
Luas permukaan kubus dapat digunakan untuk menentukan ukuran permukaan kubus, seperti luas permukaan sebuah kotak kardus atau sebuah ruangan berbentuk kubus. Hal ini penting dalam berbagai aplikasi, seperti pengemasan, konstruksi, dan desain.
-
Menghitung Volume
Luas permukaan kubus juga terkait dengan volume kubus. Dengan mengetahui luas permukaan dan panjang sisi kubus, kita dapat menghitung volume kubus menggunakan rumus V = s, di mana V adalah volume kubus.
-
Contoh dalam Kehidupan Nyata
Banyak benda dalam kehidupan nyata yang memiliki permukaan berbentuk kubus, seperti dadu, kotak kardus, dan akuarium. Memahami konsep luas permukaan kubus dapat membantu kita memahami sifat benda-benda tersebut dan menyelesaikan masalah yang melibatkan benda-benda tersebut.
Dengan memahami hubungan antara konsep luas permukaan dan berapa sisi kubus, kita dapat lebih memahami sifat-sifat kubus secara keseluruhan dan menyelesaikan masalah yang melibatkan kubus.
Contoh dalam kehidupan sehari-hari (dadu, kotak kardus, akuarium)
Dalam kehidupan sehari-hari, kita dapat menemukan banyak benda yang berbentuk kubus, seperti dadu, kotak kardus, dan akuarium. Benda-benda ini memiliki enam sisi berbentuk persegi yang sama ukuran. Dengan demikian, benda-benda tersebut merupakan contoh nyata dari kubus dalam kehidupan sehari-hari.
Memahami hubungan antara contoh-contoh dalam kehidupan sehari-hari dan konsep “berapa sisi kubus” sangat penting karena hal ini dapat membantu kita memahami sifat-sifat kubus dan menerapkannya dalam kehidupan nyata. Misalnya, kita dapat menggunakan konsep kubus untuk menghitung volume akuarium atau luas permukaan kotak kardus.
Selain itu, memahami contoh-contoh dalam kehidupan sehari-hari dapat membuat konsep kubus lebih mudah dipahami dan diingat. Dengan melihat benda-benda yang familiar seperti dadu atau kotak kardus, kita dapat lebih mudah membayangkan bentuk dan sifat-sifat kubus.
Pertanyaan Umum tentang “Berapa Sisi Kubus”
Berikut adalah beberapa pertanyaan umum dan jawabannya terkait “berapa sisi kubus”:
Pertanyaan 1: Berapa jumlah sisi kubus?
Kubus memiliki enam sisi.
Pertanyaan 2: Apa bentuk sisi-sisi kubus?
Sisi-sisi kubus berbentuk persegi.
Pertanyaan 3: Apakah semua sisi kubus sama?
Ya, semua sisi kubus sama ukuran.
Pertanyaan 4: Bagaimana cara menghitung volume kubus?
Volume kubus dapat dihitung dengan rumus Volume = sisi x sisi x sisi.
Pertanyaan 5: Bagaimana cara menghitung luas permukaan kubus?
Luas permukaan kubus dapat dihitung dengan rumus Luas permukaan = 6 x (sisi x sisi).
Pertanyaan 6: Apa saja contoh benda yang berbentuk kubus dalam kehidupan sehari-hari?
Contoh benda yang berbentuk kubus dalam kehidupan sehari-hari antara lain dadu, kotak kardus, dan akuarium.
Dengan memahami jawaban atas pertanyaan-pertanyaan umum ini, diharapkan dapat membantu dalam memahami konsep “berapa sisi kubus” dan penerapannya dalam kehidupan sehari-hari.
Untuk informasi lebih lanjut tentang kubus dan sifat-sifatnya, silakan lanjutkan membaca artikel ini.
Tips Memahami Konsep “Berapa Sisi Kubus”
Memahami konsep “berapa sisi kubus” sangat penting dalam matematika dan kehidupan sehari-hari. Berikut adalah beberapa tips untuk membantu Anda memahami konsep ini:
Tip 1: Visualisasikan Kubus
Bayangkan sebuah dadu atau kotak kardus. Hitunglah jumlah sisi pada benda-benda tersebut. Anda akan melihat bahwa kubus memiliki enam sisi.
Tip 2: Pahami Bentuk Sisi Kubus
Amati sisi-sisi kubus. Anda akan melihat bahwa semua sisi berbentuk persegi. Setiap sisi memiliki panjang yang sama.
Tip 3: Hitung Rusuk dan Titik Sudut Kubus
Hitunglah jumlah garis yang menghubungkan sisi-sisi kubus (rusuk) dan jumlah titik di mana sisi-sisi kubus bertemu (titik sudut). Anda akan menemukan bahwa kubus memiliki 12 rusuk dan 8 titik sudut.
Tip 4: Terapkan dalam Kehidupan Sehari-hari
Carilah benda-benda di sekitar Anda yang berbentuk kubus, seperti dadu, kotak kardus, atau akuarium. Identifikasi enam sisi, bentuk sisi, serta rusuk dan titik sudut pada benda-benda tersebut.
Tip 5: Berlatih Soal
Kerjakan soal-soal yang berkaitan dengan kubus. Hitunglah volume, luas permukaan, dan sifat-sifat lainnya dari kubus. Dengan berlatih, Anda akan semakin memahami konsep “berapa sisi kubus”.
Dengan mengikuti tips-tips ini, Anda akan dapat memahami konsep “berapa sisi kubus” dengan mudah dan dapat menerapkan konsep ini dalam kehidupan sehari-hari.
Lanjutkan membaca artikel ini untuk informasi lebih lanjut tentang sifat-sifat dan aplikasi kubus.
Kesimpulan
Setelah mengupas tuntas tentang “berapa sisi kubus”, dapat disimpulkan bahwa kubus adalah bangun ruang tiga dimensi yang memiliki enam sisi berbentuk persegi, dua belas rusuk, dan delapan titik sudut. Sisi-sisi kubus sama ukuran dan saling tegak lurus, sehingga kubus memiliki sifat simetri yang tinggi.
Memahami konsep “berapa sisi kubus” sangat penting dalam matematika dan kehidupan sehari-hari. Konsep ini digunakan untuk menghitung volume, luas permukaan, dan sifat-sifat lainnya dari kubus. Selain itu, konsep ini juga dapat diterapkan dalam berbagai bidang, seperti arsitektur, teknik, dan desain.
Youtube Video:
