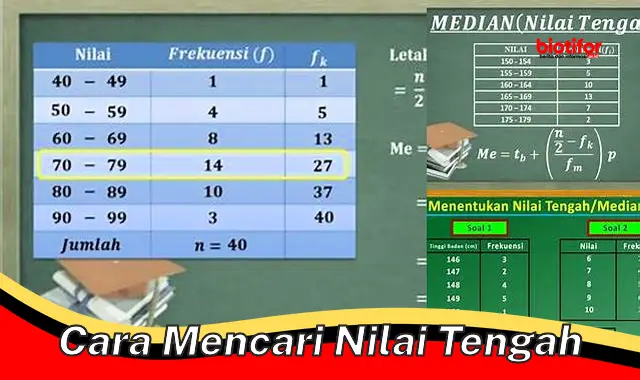
Nilai tengah atau rata-rata adalah sebuah ukuran yang menyatakan kecenderungan pusat dari suatu kelompok data. Nilai tengah dapat digunakan untuk membandingkan kelompok data yang berbeda atau untuk melacak perubahan suatu kelompok data dari waktu ke waktu.
Ada beberapa cara untuk mencari nilai tengah. Cara yang paling umum adalah dengan menjumlahkan semua data dan kemudian membagi jumlah tersebut dengan jumlah data. Cara ini disebut dengan nilai tengah aritmatika.
Selain nilai tengah aritmatika, ada juga jenis nilai tengah lainnya, seperti nilai tengah harmonik, nilai tengah geometrik, dan nilai tengah kuadrat. Jenis nilai tengah yang digunakan akan tergantung pada jenis data dan tujuan analisis.
Cara Mencari Nilai Tengah
Nilai tengah atau rata-rata merupakan ukuran penting yang menunjukkan kecenderungan pusat suatu kelompok data. Berikut adalah 9 aspek penting terkait cara mencari nilai tengah:
- Pengertian: Nilai tengah adalah ukuran yang menyatakan kecenderungan pusat dari suatu kelompok data.
- Jenis: Ada beberapa jenis nilai tengah, seperti nilai tengah aritmatika, harmonik, geometrik, dan kuadrat.
- Tujuan: Nilai tengah digunakan untuk membandingkan kelompok data atau melacak perubahan data dari waktu ke waktu.
- Rumus: Rumus untuk mencari nilai tengah aritmatika adalah jumlah semua data dibagi jumlah data.
- Aplikasi: Nilai tengah digunakan dalam berbagai bidang, seperti statistik, keuangan, dan sains.
- Keterbatasan: Nilai tengah dapat menyesatkan jika data memiliki pencilan atau distribusi yang tidak normal.
- Interpretasi: Nilai tengah harus diinterpretasikan dalam konteks data dan tujuan analisis.
- Contoh: Jika nilai ujian siswa adalah 80, 90, dan 70, maka nilai tengahnya adalah 80.
- Relevansi: Nilai tengah merupakan ukuran dasar yang penting untuk memahami dan menganalisis data.
Dengan memahami berbagai aspek ini, kita dapat menggunakan nilai tengah secara efektif untuk membuat keputusan yang lebih baik dan menarik kesimpulan yang lebih akurat dari data yang tersedia.
Pengertian
Pengertian nilai tengah sangat penting dalam memahami cara mencari nilai tengah. Nilai tengah merupakan ukuran yang menunjukkan kecenderungan pusat dari suatu kelompok data, sehingga menjadi dasar untuk menghitung nilai tengah dengan benar.
-
Komponen Nilai Tengah
Nilai tengah terdiri dari dua komponen utama, yaitu jumlah semua data dan jumlah data. Kedua komponen ini saling terkait, sehingga perubahan pada salah satu komponen akan mempengaruhi nilai tengah. -
Jenis Nilai Tengah
Dalam praktiknya, ada beberapa jenis nilai tengah yang dapat digunakan, tergantung pada jenis data dan tujuan analisis. Memahami jenis-jenis nilai tengah ini penting untuk memilih metode perhitungan yang tepat. -
Interpretasi Nilai Tengah
Nilai tengah harus diinterpretasikan dengan hati-hati, dengan mempertimbangkan konteks data dan tujuan analisis. Nilai tengah dapat menyesatkan jika data memiliki pencilan atau distribusi yang tidak normal.
Dengan memahami pengertian nilai tengah secara mendalam, kita dapat menerapkan cara mencari nilai tengah dengan lebih efektif dan akurat. Pemahaman ini menjadi dasar penting untuk melakukan analisis data yang valid dan dapat diandalkan.
Jenis
Jenis nilai tengah memegang peranan penting dalam “cara mencari nilai tengah” karena menentukan metode perhitungan yang tepat. Berbagai jenis nilai tengah memiliki rumus dan aplikasi yang berbeda, sehingga memilih jenis nilai tengah yang sesuai sangat krusial untuk mendapatkan hasil yang akurat.
Misalnya, nilai tengah aritmatika cocok untuk data yang memiliki distribusi normal, sedangkan nilai tengah harmonik berguna untuk data yang memiliki nilai nol atau negatif. Nilai tengah geometrik digunakan untuk data yang menunjukkan pertumbuhan atau penurunan secara eksponensial, dan nilai tengah kuadrat cocok untuk data yang berkaitan dengan jarak atau selisih.
Dengan memahami jenis-jenis nilai tengah dan cara memilih jenis yang tepat, kita dapat menerapkan “cara mencari nilai tengah” secara lebih efektif dan tepat sasaran. Hal ini sangat penting dalam berbagai bidang, seperti statistik, keuangan, dan sains, di mana analisis data yang akurat sangat krusial untuk pengambilan keputusan yang tepat.
Tujuan
Tujuan penggunaan nilai tengah sangat terkait dengan “cara mencari nilai tengah” itu sendiri. Mengetahui tujuan penggunaan nilai tengah membantu kita menentukan cara yang tepat untuk menghitungnya dan menginterpretasikan hasilnya.
-
Perbandingan Kelompok Data
Nilai tengah memungkinkan kita membandingkan dua atau lebih kelompok data dengan ringkas dan efisien. Dengan menghitung nilai tengah setiap kelompok, kita dapat dengan cepat mengidentifikasi kelompok yang memiliki nilai rata-rata lebih tinggi atau lebih rendah. Perbandingan ini sangat berguna dalam berbagai bidang, seperti penelitian, pemasaran, dan keuangan. -
Pelacakan Perubahan Data
Nilai tengah juga berguna untuk melacak perubahan data dari waktu ke waktu. Dengan menghitung nilai tengah data pada periode waktu yang berbeda, kita dapat mengidentifikasi tren atau pola perubahan. Pelacakan perubahan data ini penting untuk memantau kemajuan, mengevaluasi efektivitas program, dan membuat prediksi.
Dengan memahami tujuan penggunaan nilai tengah, kita dapat memilih cara yang tepat untuk menghitungnya dan memperoleh wawasan yang berharga dari data yang kita miliki. Nilai tengah menjadi alat yang sangat berharga dalam analisis data, membantu kita membandingkan kelompok data dan melacak perubahan dari waktu ke waktu secara efektif.
Rumus
Rumus ini merupakan inti dari “cara mencari nilai tengah”, khususnya untuk nilai tengah aritmatika. Rumus ini menetapkan langkah-langkah jelas untuk menghitung nilai tengah, menjadikannya dasar bagi metode perhitungan nilai tengah lainnya.
-
Komponen Rumus
Rumus nilai tengah aritmatika terdiri dari dua komponen utama: jumlah semua data dan jumlah data. Kedua komponen ini memiliki peran penting dalam menentukan nilai tengah. -
Penerapan Rumus
Rumus nilai tengah aritmatika dapat diterapkan pada berbagai jenis data, mulai dari data numerik hingga data kategorikal. Penerapan rumus ini sangat luas, mulai dari bidang pendidikan hingga penelitian ilmiah. -
Interpretasi Hasil
Hasil perhitungan nilai tengah aritmatika harus diinterpretasikan dengan hati-hati, dengan mempertimbangkan konteks data dan tujuan analisis. Interpretasi yang tepat akan menghasilkan kesimpulan yang valid dan bermakna. -
Keterbatasan Rumus
Meskipun sederhana dan mudah digunakan, rumus nilai tengah aritmatika memiliki keterbatasan. Misalnya, rumus ini dapat terpengaruh oleh adanya pencilan atau distribusi data yang tidak normal.
Dengan memahami rumus nilai tengah aritmatika dan keterbatasannya, kita dapat menggunakan “cara mencari nilai tengah” secara efektif dan akurat. Rumus ini menjadi alat dasar yang sangat penting dalam analisis data dan pengambilan keputusan yang tepat.
Aplikasi
Nilai tengah memiliki peran penting dalam berbagai bidang karena memberikan dasar pengukuran dan perbandingan data. Dalam statistik, nilai tengah digunakan untuk meringkas data dan membuat inferensi tentang populasi yang lebih besar. Dalam keuangan, nilai tengah digunakan untuk menghitung rata-rata pengembalian investasi dan mengelola risiko. Dalam sains, nilai tengah digunakan untuk menganalisis hasil eksperimen dan menarik kesimpulan tentang fenomena alam.
Cara mencari nilai tengah sangat penting dalam konteks aplikasi ini karena memastikan bahwa nilai tengah yang dihitung akurat dan dapat diandalkan. Jika nilai tengah dihitung secara tidak tepat, maka kesimpulan dan keputusan yang diambil berdasarkan nilai tengah tersebut dapat menyesatkan atau salah.
Oleh karena itu, memahami cara mencari nilai tengah dengan benar sangat penting untuk memastikan bahwa nilai tengah yang digunakan dalam berbagai aplikasi memberikan informasi yang valid dan bermanfaat. Tanpa pemahaman yang kuat tentang cara mencari nilai tengah, aplikasi nilai tengah dalam berbagai bidang dapat menjadi tidak efektif atau bahkan berbahaya.
Keterbatasan
Pemahaman tentang keterbatasan nilai tengah sangat penting dalam konteks “cara mencari nilai tengah” karena membantu kita mengidentifikasi situasi di mana nilai tengah mungkin tidak memberikan representasi akurat dari data. Pencilan, atau data yang sangat berbeda dari nilai lainnya, dan distribusi data yang tidak normal dapat memengaruhi nilai tengah secara signifikan, sehingga menghasilkan kesimpulan yang menyesatkan.
Misalnya, jika kita memiliki data nilai ujian dengan pencilan berupa nilai yang sangat tinggi, nilai tengah akan meningkat secara tidak proporsional, memberikan kesan yang salah tentang kinerja keseluruhan siswa. Demikian pula, jika data didistribusikan secara tidak normal, seperti dalam kasus data penghasilan, di mana sebagian besar orang berpenghasilan rendah dan hanya sedikit yang berpenghasilan sangat tinggi, nilai tengah dapat memberikan gambaran yang terdistorsi tentang pendapatan rata-rata.
Oleh karena itu, penting untuk mempertimbangkan distribusi data dan keberadaan pencilan sebelum menggunakan nilai tengah. Jika data memiliki banyak pencilan atau distribusi yang tidak normal, metode lain seperti median atau modus mungkin lebih tepat untuk meringkas data.
Dengan memahami keterbatasan nilai tengah dan cara mengatasinya, kita dapat menggunakan “cara mencari nilai tengah” secara lebih efektif dan akurat. Pemahaman ini sangat penting untuk memastikan bahwa kita memperoleh wawasan yang bermakna dan dapat diandalkan dari data yang kita analisis.
Interpretasi
Interpretasi nilai tengah merupakan komponen penting dalam “cara mencari nilai tengah” karena menyediakan pemahaman yang lebih mendalam tentang makna dan signifikansi nilai tengah yang dihitung. Menafsirkan nilai tengah dalam konteks data dan tujuan analisis memastikan bahwa kita memperoleh kesimpulan yang valid dan bermakna dari data.
Misalnya, jika kita menghitung nilai tengah nilai ujian siswa, kita perlu mempertimbangkan tingkat kesulitan ujian dan kemampuan siswa saat menafsirkan nilai tengah. Nilai tengah yang tinggi mungkin menunjukkan bahwa siswa telah menguasai materi dengan baik, atau mungkin ujian tersebut terlalu mudah. Sebaliknya, nilai tengah yang rendah mungkin menunjukkan bahwa siswa masih kesulitan memahami materi, atau mungkin ujian tersebut terlalu sulit.
Dengan memahami pentingnya interpretasi nilai tengah, kita dapat menggunakan “cara mencari nilai tengah” secara lebih efektif. Interpretasi yang tepat membantu kita mengidentifikasi pola dan tren dalam data, membuat perbandingan yang bermakna, dan menarik kesimpulan yang didukung oleh bukti. Selain itu, interpretasi nilai tengah juga membantu kita mengidentifikasi area di mana diperlukan perbaikan atau tindakan lebih lanjut.
Dengan menggabungkan interpretasi nilai tengah ke dalam “cara mencari nilai tengah”, kita dapat memperoleh pemahaman yang lebih komprehensif tentang data dan membuat keputusan yang lebih tepat berdasarkan data tersebut.
Contoh
Contoh ini merupakan ilustrasi langsung dari “cara mencari nilai tengah” menggunakan nilai tengah aritmatika. Nilai tengah aritmatika dihitung dengan menjumlahkan semua nilai data dan membaginya dengan jumlah data. Dalam contoh ini, kita memiliki tiga nilai data: 80, 90, dan 70. Menjumlahkan ketiga nilai ini menghasilkan 240. Membagi 240 dengan 3 (jumlah data) menghasilkan nilai tengah 80.
Contoh ini penting karena menunjukkan langkah-langkah praktis dalam menghitung nilai tengah. Ini memperkuat pemahaman tentang rumus nilai tengah aritmatika dan bagaimana rumus tersebut digunakan untuk memperoleh nilai tengah dari satu set data tertentu. Selain itu, contoh ini menyoroti pentingnya menggunakan nilai tengah sebagai ukuran kecenderungan pusat dari suatu kelompok data.
Dalam konteks yang lebih luas, memahami cara menghitung nilai tengah sangat penting dalam berbagai bidang, seperti statistik, penelitian, dan pengambilan keputusan. Nilai tengah memberikan ringkasan numerik dari suatu kelompok data, memungkinkan perbandingan antara kelompok data yang berbeda dan identifikasi tren atau pola dalam data dari waktu ke waktu.
Relevansi
Nilai tengah merupakan ukuran dasar yang penting untuk memahami dan menganalisis data karena memberikan ringkasan numerik dari suatu kelompok data, yang memungkinkan kita untuk:
-
Membandingkan kelompok data yang berbeda
Nilai tengah memungkinkan kita membandingkan kecenderungan pusat dari dua atau lebih kelompok data, mengidentifikasi kelompok dengan nilai rata-rata lebih tinggi atau lebih rendah. -
Melacak perubahan data dari waktu ke waktu
Dengan menghitung nilai tengah data pada periode waktu yang berbeda, kita dapat mengidentifikasi tren atau pola perubahan, memantau kemajuan, dan mengevaluasi efektivitas program tertentu. -
Mengidentifikasi pencilan dan data yang tidak biasa
Nilai tengah yang sangat berbeda dari nilai data lainnya dapat menunjukkan adanya pencilan atau data yang tidak biasa, yang perlu diselidiki lebih lanjut untuk memahami implikasinya. -
Membuat prediksi dan perkiraan
Nilai tengah dapat digunakan sebagai dasar untuk membuat prediksi dan perkiraan tentang data di masa mendatang, dengan mempertimbangkan tren dan pola masa lalu.
Memahami cara mencari nilai tengah sangat penting untuk memanfaatkan kekuatan nilai tengah dalam memahami dan menganalisis data secara efektif. Dengan menghitung nilai tengah menggunakan metode yang tepat dan menafsirkannya dengan benar, kita dapat memperoleh wawasan berharga dari data yang kita miliki dan membuat keputusan yang lebih tepat berdasarkan informasi.
Pertanyaan Umum tentang “Cara Mencari Nilai Tengah”
Berikut adalah beberapa pertanyaan umum dan jawabannya terkait “cara mencari nilai tengah”:
Pertanyaan 1: Apa itu nilai tengah?
Nilai tengah adalah ukuran yang menyatakan kecenderungan pusat dari suatu kelompok data. Ini memberikan ringkasan numerik dari data, memudahkan perbandingan dan analisis.
Pertanyaan 2: Bagaimana cara mencari nilai tengah?
Nilai tengah dapat dicari dengan menjumlahkan semua nilai data dan membaginya dengan jumlah data. Metode ini dikenal sebagai nilai tengah aritmatika.
Pertanyaan 3: Kapan nilai tengah tidak tepat digunakan?
Nilai tengah tidak tepat digunakan ketika data memiliki pencilan atau distribusi yang tidak normal. Dalam kasus ini, median atau modus mungkin lebih tepat.
Pertanyaan 4: Apa saja jenis nilai tengah?
Selain nilai tengah aritmatika, ada juga jenis nilai tengah lainnya, seperti nilai tengah harmonik, geometrik, dan kuadrat. Jenis nilai tengah yang digunakan tergantung pada jenis data dan tujuan analisis.
Pertanyaan 5: Mengapa nilai tengah penting?
Nilai tengah penting karena memberikan ukuran kecenderungan pusat, memungkinkan perbandingan data, pelacakan perubahan, dan identifikasi pola.
Pertanyaan 6: Bagaimana cara menginterpretasikan nilai tengah?
Nilai tengah harus diinterpretasikan dalam konteks data dan tujuan analisis. Penting untuk mempertimbangkan distribusi data dan keberadaan pencilan saat menafsirkan nilai tengah.
Dengan memahami pertanyaan umum ini, kita dapat menggunakan “cara mencari nilai tengah” secara efektif dan akurat untuk memperoleh wawasan berharga dari data.
Beranda
Tips Mencari Nilai Tengah
Berikut adalah beberapa tips untuk mencari nilai tengah secara efektif dan akurat:
Periksa Distribusi Data: Sebelum menghitung nilai tengah, periksa distribusi data untuk mengidentifikasi adanya pencilan atau distribusi yang tidak normal. Hal ini penting karena pencilan dapat memengaruhi nilai tengah secara signifikan.
Pilih Jenis Nilai Tengah yang Tepat: Ada beberapa jenis nilai tengah, seperti aritmatika, harmonik, geometrik, dan kuadrat. Pilih jenis nilai tengah yang sesuai dengan jenis data dan tujuan analisis.
Gunakan Rumus yang Benar: Pastikan menggunakan rumus yang benar untuk menghitung nilai tengah. Rumus yang paling umum digunakan adalah nilai tengah aritmatika, yang dihitung dengan menjumlahkan semua nilai data dan membaginya dengan jumlah data.
Interpretasikan Nilai Tengah dengan Hati-hati: Nilai tengah harus diinterpretasikan dengan hati-hati, dengan mempertimbangkan konteks data dan tujuan analisis. Pencilan dan distribusi data yang tidak normal dapat memengaruhi interpretasi nilai tengah.
Gunakan Kalkulator atau Perangkat Lunak: Untuk menghitung nilai tengah dari kumpulan data yang besar, pertimbangkan untuk menggunakan kalkulator atau perangkat lunak statistik. Hal ini dapat menghemat waktu dan meminimalkan kesalahan perhitungan.
Dengan mengikuti tips ini, Anda dapat mencari nilai tengah secara efektif dan akurat, sehingga memperoleh wawasan berharga dari data Anda.
Kembali ke Artikel Utama
Kesimpulan
Memahami “cara mencari nilai tengah” sangat penting untuk menganalisis dan memahami data secara efektif. Nilai tengah memberikan ukuran kecenderungan pusat, memungkinkan kita membandingkan data, mengidentifikasi tren, dan membuat prediksi. Dengan memilih jenis nilai tengah yang tepat, menggunakan rumus yang benar, dan menafsirkan hasil dengan hati-hati, kita dapat memperoleh wawasan berharga dari data yang tersedia.
Nilai tengah memiliki peran penting dalam berbagai bidang, mulai dari statistik hingga sains dan keuangan. Memahami cara mencari nilai tengah memberdayakan kita untuk mengevaluasi data secara kritis, membuat keputusan berdasarkan informasi, dan berkontribusi pada kemajuan pengetahuan.
Youtube Video:
