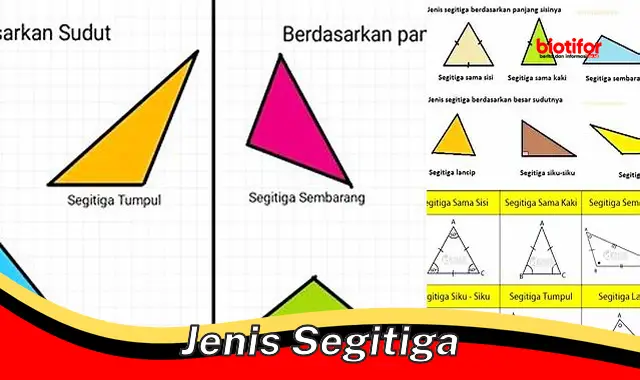
Segitiga adalah bangun datar dua dimensi yang memiliki tiga sisi dan tiga sudut. Jenis-jenis segitiga ditentukan berdasarkan panjang sisi dan besar sudutnya. Berdasarkan panjang sisinya, segitiga dapat dibedakan menjadi segitiga sama sisi, segitiga sama kaki, dan segitiga sembarang. Berdasarkan besar sudutnya, segitiga dapat dibedakan menjadi segitiga lancip, segitiga siku-siku, dan segitiga tumpul.
Segitiga memiliki banyak kegunaan dalam kehidupan sehari-hari. Salah satu kegunaan yang paling umum adalah untuk mengukur jarak dan tinggi benda. Segitiga juga digunakan dalam konstruksi, arsitektur, dan teknik. Dalam matematika, segitiga banyak digunakan dalam geometri dan trigonometri.
Berikut adalah beberapa topik utama yang akan dibahas dalam artikel ini:
- Jenis-jenis segitiga
- Sifat-sifat segitiga
- Kegunaan segitiga
Jenis Segitiga
Segitiga adalah bangun datar dua dimensi yang memiliki tiga sisi dan tiga sudut. Jenis-jenis segitiga ditentukan berdasarkan panjang sisi dan besar sudutnya, yang menjadi aspek penting dalam memahami segitiga.
- Jenis berdasarkan panjang sisi: Segitiga sama sisi, sama kaki, sembarang
- Jenis berdasarkan besar sudut: Segitiga lancip, siku-siku, tumpul
- Sifat sudut: Jumlah sudut dalam segitiga = 180 derajat
- Sifat sisi: Jumlah dua sisi lebih besar dari sisi lainnya
- Luas: 1/2 alas x tinggi
- Keliling: Jumlah panjang semua sisi
- Teorema Pythagoras: a + b = c (untuk segitiga siku-siku)
- Trigonometri: Sinus, kosinus, tangen untuk menghitung sisi dan sudut segitiga
Kedelapan aspek tersebut saling berkaitan dan membentuk dasar pemahaman tentang segitiga. Misalnya, jenis segitiga berdasarkan panjang sisi menentukan sifat sudutnya, yang kemudian dapat digunakan untuk menghitung luas dan keliling segitiga menggunakan rumus yang sesuai. Teorema Pythagoras sangat penting untuk menyelesaikan masalah segitiga siku-siku, sedangkan trigonometri memungkinkan kita menghitung sisi dan sudut segitiga apa pun.
Jenis Berdasarkan Panjang Sisi
Jenis segitiga berdasarkan panjang sisi merupakan aspek krusial dalam memahami karakteristik dan sifat segitiga. Berdasarkan panjang sisinya, segitiga dapat diklasifikasikan menjadi tiga jenis, yaitu segitiga sama sisi, sama kaki, dan sembarang.
-
Segitiga Sama Sisi
Segitiga sama sisi adalah segitiga yang memiliki ketiga sisinya sama panjang. Sifat khusus segitiga sama sisi adalah ketiga sudutnya juga sama besar, yaitu 60 derajat. Dalam kehidupan nyata, segitiga sama sisi dapat ditemukan pada bentuk sarang lebah atau atap rumah tradisional Jepang.
-
Segitiga Sama Kaki
Segitiga sama kaki memiliki dua sisi yang sama panjang dan satu sisi yang berbeda panjang. Sudut yang berhadapan dengan sisi yang berbeda panjang akan sama besar. Segitiga sama kaki banyak digunakan dalam konstruksi jembatan dan rangka atap karena sifatnya yang stabil.
-
Segitiga Sembarang
Segitiga sembarang adalah segitiga yang tidak memiliki sisi yang sama panjang. Ketiga sisi dan sudutnya memiliki ukuran yang berbeda-beda. Segitiga sembarang banyak ditemukan pada bentuk benda-benda alam, seperti daun dan gunung.
Klasifikasi segitiga berdasarkan panjang sisi ini sangat penting karena menentukan sifat-sifat lain dari segitiga, seperti jenis sudutnya, luas, dan kelilingnya. Dengan memahami jenis segitiga berdasarkan panjang sisinya, kita dapat menganalisis dan menyelesaikan berbagai masalah terkait segitiga dengan lebih mudah dan akurat.
Jenis Berdasarkan Besar Sudut
Jenis segitiga berdasarkan besar sudut merupakan aspek penting lainnya dalam memahami segitiga. Berdasarkan besar sudutnya, segitiga dapat diklasifikasikan menjadi segitiga lancip, siku-siku, dan tumpul.
-
Segitiga Lancip
Segitiga lancip adalah segitiga yang memiliki ketiga sudutnya kurang dari 90 derajat. Segitiga lancip banyak ditemukan pada bentuk atap rumah dan tenda karena bentuknya yang runcing.
-
Segitiga Siku-siku
Segitiga siku-siku adalah segitiga yang memiliki salah satu sudutnya sebesar 90 derajat. Segitiga siku-siku banyak digunakan dalam konstruksi dan teknik karena sifatnya yang stabil dan mudah diukur.
-
Segitiga Tumpul
Segitiga tumpul adalah segitiga yang memiliki salah satu sudutnya lebih besar dari 90 derajat. Segitiga tumpul banyak ditemukan pada bentuk perbukitan dan atap gedung yang melengkung.
Selain menentukan bentuk dan sifat segitiga, jenis segitiga berdasarkan besar sudut juga memiliki implikasi dalam perhitungan luas dan keliling segitiga. Dengan memahami jenis segitiga berdasarkan besar sudutnya, kita dapat menganalisis dan menyelesaikan berbagai masalah terkait segitiga dengan lebih mudah dan akurat.
Sifat sudut
Sifat sudut pada segitiga, yaitu jumlah sudut dalam segitiga adalah 180 derajat, merupakan konsep dasar yang sangat penting dalam geometri. Sifat ini memiliki hubungan yang erat dengan jenis segitiga dan memiliki implikasi yang luas dalam memahami segitiga.
-
Pengaruh pada jenis segitiga
Sifat jumlah sudut dalam segitiga 180 derajat memengaruhi jenis segitiga berdasarkan besar sudutnya. Pada segitiga lancip, ketiga sudutnya kurang dari 90 derajat, sehingga jumlahnya kurang dari 180 derajat. Pada segitiga siku-siku, salah satu sudutnya 90 derajat, sehingga jumlah dua sudut lainnya adalah 90 derajat. Sedangkan pada segitiga tumpul, salah satu sudutnya lebih dari 90 derajat, sehingga jumlah dua sudut lainnya kurang dari 90 derajat.
-
Perhitungan sudut segitiga
Sifat jumlah sudut dalam segitiga 180 derajat dapat digunakan untuk menghitung besar sudut segitiga jika diketahui dua sudut lainnya. Misalnya, jika diketahui sebuah segitiga memiliki dua sudut yang besarnya 60 derajat dan 70 derajat, maka sudut ketiga dapat dihitung dengan mengurangi jumlah kedua sudut tersebut dari 180 derajat, yaitu 180 derajat – 60 derajat – 70 derajat = 50 derajat.
-
Penerapan dalam kehidupan nyata
Sifat jumlah sudut dalam segitiga 180 derajat memiliki banyak penerapan dalam kehidupan nyata. Misalnya, dalam konstruksi, sifat ini digunakan untuk memastikan bahwa sudut-sudut bangunan siku-siku atau memiliki besar yang diinginkan. Dalam navigasi, sifat ini digunakan untuk menentukan arah dan posisi.
Secara keseluruhan, sifat sudut pada segitiga, yaitu jumlah sudut dalam segitiga adalah 180 derajat, merupakan konsep dasar yang sangat penting dalam memahami jenis segitiga dan memiliki banyak aplikasi dalam kehidupan nyata. Dengan memahami sifat ini, kita dapat menganalisis dan menyelesaikan masalah terkait segitiga dengan lebih mudah dan akurat.
Sifat sisi
Sifat sisi pada segitiga, yaitu jumlah dua sisi lebih besar dari sisi lainnya, merupakan konsep dasar yang sangat penting dalam geometri. Sifat ini memiliki hubungan yang erat dengan jenis segitiga dan memiliki implikasi yang luas dalam memahami segitiga.
Sifat ini menentukan kondisi keberadaan sebuah segitiga. Sebuah segitiga dapat terbentuk jika memenuhi sifat ini, yaitu jumlah panjang dua sisi manapun harus lebih besar dari panjang sisi yang ketiga. Sebaliknya, jika sifat ini tidak terpenuhi, maka segitiga tidak dapat terbentuk.
Sifat jumlah dua sisi lebih besar dari sisi lainnya juga memiliki implikasi dalam menentukan jenis segitiga. Misalnya, pada segitiga sama sisi, ketiga sisinya memiliki panjang yang sama, sehingga sifat ini selalu terpenuhi. Pada segitiga sama kaki, dua sisinya memiliki panjang yang sama, sehingga sifat ini juga selalu terpenuhi. Sedangkan pada segitiga sembarang, ketiga sisinya memiliki panjang yang berbeda-beda, sehingga sifat ini hanya terpenuhi untuk dua pasang sisi segitiga.
Secara keseluruhan, sifat sisi pada segitiga, yaitu jumlah dua sisi lebih besar dari sisi lainnya, merupakan konsep dasar yang sangat penting dalam memahami jenis segitiga dan memiliki banyak aplikasi dalam kehidupan nyata. Dengan memahami sifat ini, kita dapat menganalisis dan menyelesaikan masalah terkait segitiga dengan lebih mudah dan akurat.
Luas
Rumus luas segitiga yaitu 1/2 alas x tinggi memiliki kaitan yang erat dengan jenis segitiga. Rumus ini berlaku untuk semua jenis segitiga, baik segitiga sama sisi, sama kaki, maupun sembarang. Namun, jenis segitiga memengaruhi nilai alas dan tinggi yang digunakan dalam rumus tersebut.
-
Jenis segitiga dan alas
Alas pada rumus luas segitiga adalah panjang sisi yang tegak lurus dengan tinggi. Untuk segitiga sama sisi, ketiga sisinya sama panjang, sehingga alasnya dapat berupa sisi manapun. Untuk segitiga sama kaki, alasnya adalah sisi yang tidak sama panjang. Sedangkan untuk segitiga sembarang, alasnya dapat berupa sisi manapun.
-
Jenis segitiga dan tinggi
Tinggi pada rumus luas segitiga adalah panjang garis yang ditarik dari titik sudut ke alas dan tegak lurus terhadap alas. Untuk segitiga sama sisi, tinggi dapat ditarik dari titik sudut manapun ke alas manapun. Untuk segitiga sama kaki, tinggi ditarik dari titik sudut yang berhadapan dengan sisi yang tidak sama panjang ke alas. Sedangkan untuk segitiga sembarang, tinggi dapat ditarik dari titik sudut manapun ke alas manapun.
-
Contoh
Misalkan kita memiliki sebuah segitiga sama sisi dengan panjang sisi 10 cm. Untuk menghitung luas segitiga tersebut, kita dapat menggunakan rumus luas segitiga dengan alas dan tinggi yang sama, yaitu 1/2 x 10 cm x 10 cm = 50 cm2.
Dengan memahami kaitan antara rumus luas segitiga dengan jenis segitiga, kita dapat menghitung luas segitiga dengan lebih mudah dan akurat. Pemahaman ini juga penting untuk menyelesaikan berbagai masalah matematika yang melibatkan segitiga.
Keliling
Keliling segitiga merupakan aspek penting yang berkaitan erat dengan jenis segitiga. Keliling didefinisikan sebagai jumlah panjang dari ketiga sisi segitiga.
-
Pengaruh jenis segitiga pada keliling
Jenis segitiga memengaruhi nilai kelilingnya. Pada segitiga sama sisi, ketiga sisinya memiliki panjang yang sama, sehingga rumus kelilingnya menjadi: K = 3 x s, dengan s adalah panjang sisi segitiga. Pada segitiga sama kaki, dua sisinya memiliki panjang yang sama, sehingga rumus kelilingnya menjadi: K = 2 x s1 + s2, dengan s1 adalah panjang sisi yang sama dan s2 adalah panjang sisi yang berbeda. Sedangkan pada segitiga sembarang, ketiga sisinya memiliki panjang yang berbeda, sehingga rumus kelilingnya menjadi: K = s1 + s2 + s3, dengan s1, s2, dan s3 adalah panjang ketiga sisi segitiga.
-
Contoh penerapan dalam kehidupan nyata
Konsep keliling segitiga banyak diterapkan dalam kehidupan nyata, seperti dalam konstruksi dan arsitektur. Dalam membangun sebuah rumah, arsitek perlu menghitung keliling segitiga untuk menentukan jumlah bahan yang dibutuhkan untuk membuat rangka atap atau dinding.
-
Hubungan dengan sifat segitiga
Keliling segitiga juga memiliki hubungan dengan sifat-sifat segitiga lainnya, seperti luas dan tinggi. Misalnya, dalam segitiga sama sisi, kelilingnya sama dengan tiga kali panjang sisi, yang juga merupakan tinggi segitiga tersebut.
Dengan memahami hubungan antara keliling dan jenis segitiga, kita dapat menghitung keliling segitiga dengan lebih mudah dan akurat. Pemahaman ini juga penting untuk menyelesaikan berbagai masalah matematika yang melibatkan segitiga.
Teorema Pythagoras
Salah satu sifat penting dari segitiga siku-siku adalah Teorema Pythagoras, yang menyatakan bahwa kuadrat panjang sisi miring (c) sama dengan jumlah kuadrat panjang kedua sisi lainnya (a dan b), atau dalam persamaan: a + b = c.
Teorema Pythagoras memiliki peran penting dalam menentukan jenis segitiga. Segitiga siku-siku didefinisikan sebagai segitiga yang memiliki satu sudut siku-siku (90 derajat). Dengan menggunakan Teorema Pythagoras, kita dapat memastikan apakah suatu segitiga merupakan segitiga siku-siku atau bukan.
Dalam kehidupan nyata, Teorema Pythagoras memiliki banyak aplikasi, seperti dalam konstruksi dan teknik. Misalnya, dalam membuat rangka atap, tukang bangunan menggunakan Teorema Pythagoras untuk memastikan bahwa sudut-sudut atap siku-siku dan rangka atap kokoh.
Memahami hubungan antara Teorema Pythagoras dan jenis segitiga sangat penting untuk menyelesaikan berbagai masalah matematika dan aplikasi praktis. Dengan memahami sifat ini, kita dapat mengidentifikasi jenis segitiga, menghitung panjang sisi yang tidak diketahui, dan menyelesaikan berbagai permasalahan yang melibatkan segitiga.
Trigonometri
Trigonometri adalah cabang matematika yang mempelajari hubungan antara sisi dan sudut segitiga. Dalam trigonometri, terdapat tiga fungsi utama, yaitu sinus, kosinus, dan tangen, yang digunakan untuk menghitung sisi dan sudut segitiga.
-
Menghitung Sisi Segitiga
Fungsi sinus, kosinus, dan tangen dapat digunakan untuk menghitung panjang sisi segitiga jika diketahui sudut dan panjang sisi lainnya. Misalnya, jika kita mengetahui besar sudut dan panjang sisi miring sebuah segitiga siku-siku, kita dapat menggunakan fungsi sinus untuk menghitung panjang sisi lainnya.
-
Menghitung Sudut Segitiga
Fungsi sinus, kosinus, dan tangen juga dapat digunakan untuk menghitung besar sudut segitiga jika diketahui panjang sisi-sisinya. Misalnya, jika kita mengetahui panjang ketiga sisi sebuah segitiga, kita dapat menggunakan fungsi kosinus untuk menghitung besar salah satu sudutnya.
-
Jenis-jenis Segitiga
Trigonometri dapat digunakan untuk menentukan jenis segitiga berdasarkan panjang sisi dan besar sudutnya. Misalnya, jika kita mengetahui panjang ketiga sisi sebuah segitiga, kita dapat menggunakan teorema Pythagoras untuk menentukan apakah segitiga tersebut siku-siku, sama sisi, atau sembarang.
Pemahaman tentang trigonometri dan hubungannya dengan jenis segitiga sangat penting dalam berbagai bidang, seperti matematika, fisika, dan teknik. Dengan memahami konsep ini, kita dapat menyelesaikan berbagai masalah yang melibatkan segitiga dengan lebih mudah dan akurat.
Tanya Jawab tentang Jenis Segitiga
Berikut ini adalah beberapa pertanyaan umum dan jawabannya mengenai jenis segitiga:
Pertanyaan 1: Apa yang dimaksud dengan segitiga?
Segitiga adalah bangun datar dua dimensi yang memiliki tiga sisi dan tiga sudut.
Pertanyaan 2: Apa saja jenis-jenis segitiga?
Jenis-jenis segitiga dapat diklasifikasikan berdasarkan panjang sisi dan besar sudutnya. Berdasarkan panjang sisi, segitiga dibagi menjadi segitiga sama sisi, sama kaki, dan sembarang. Berdasarkan besar sudutnya, segitiga dibagi menjadi segitiga lancip, siku-siku, dan tumpul.
Pertanyaan 3: Bagaimana cara menentukan jenis segitiga?
Jenis segitiga dapat ditentukan dengan mengukur panjang sisi dan besar sudutnya. Untuk segitiga sama sisi, ketiga sisinya sama panjang. Untuk segitiga sama kaki, dua sisinya sama panjang. Untuk segitiga sembarang, ketiga sisinya berbeda panjang. Untuk segitiga lancip, ketiga sudutnya kurang dari 90 derajat. Untuk segitiga siku-siku, salah satu sudutnya 90 derajat. Untuk segitiga tumpul, salah satu sudutnya lebih dari 90 derajat.
Pertanyaan 4: Apa sifat-sifat segitiga?
Sifat-sifat segitiga meliputi jumlah sudut dalam segitiga adalah 180 derajat, jumlah dua sisi lebih besar dari sisi lainnya, luas segitiga sama dengan 1/2 alas x tinggi, dan keliling segitiga sama dengan jumlah panjang ketiga sisinya.
Pertanyaan 5: Apa saja aplikasi segitiga dalam kehidupan nyata?
Segitiga memiliki banyak aplikasi dalam kehidupan nyata, seperti dalam konstruksi, arsitektur, teknik, dan navigasi.
Pertanyaan 6: Mengapa memahami jenis segitiga itu penting?
Memahami jenis segitiga sangat penting karena membantu kita dalam menyelesaikan masalah yang berkaitan dengan segitiga, seperti menghitung luas, keliling, dan sudut segitiga.
Dengan memahami jenis-jenis segitiga dan sifat-sifatnya, kita dapat menyelesaikan berbagai permasalahan yang melibatkan segitiga dengan lebih mudah dan akurat.
Artikel Terkait: Jenis-jenis Bangun Datar Lainnya
Tips Mengenal Jenis Segitiga
Memahami jenis-jenis segitiga sangat penting dalam matematika dan memiliki banyak aplikasi dalam kehidupan nyata. Berikut adalah beberapa tips untuk membantu Anda mengenali jenis segitiga:
Tip 1: Perhatikan panjang sisinya
Segitiga sama sisi memiliki ketiga sisi yang sama panjang, segitiga sama kaki memiliki dua sisi yang sama panjang, dan segitiga sembarang memiliki ketiga sisi yang berbeda panjang.
Tip 2: Ukur besar sudutnya
Segitiga lancip memiliki ketiga sudutnya kurang dari 90 derajat, segitiga siku-siku memiliki salah satu sudutnya 90 derajat, dan segitiga tumpul memiliki salah satu sudutnya lebih dari 90 derajat.
Tip 3: Gunakan sifat-sifat segitiga
Jumlah sudut dalam segitiga selalu 180 derajat, jumlah dua sisi lebih besar dari sisi lainnya, luas segitiga sama dengan 1/2 alas x tinggi, dan keliling segitiga sama dengan jumlah panjang ketiga sisinya.
Tip 4: Terapkan teorema Pythagoras
Teorema Pythagoras hanya berlaku untuk segitiga siku-siku, yaitu a + b = c, dengan a dan b adalah panjang sisi-sisi yang siku-siku dan c adalah panjang sisi miring.
Tip 5: Gunakan trigonometri
Trigonometri dapat digunakan untuk menghitung sisi dan sudut segitiga jika diketahui informasi yang cukup, seperti panjang sisi atau besar sudut lainnya.
Dengan mengikuti tips ini, Anda dapat dengan mudah mengenali jenis segitiga dan menyelesaikan masalah yang berkaitan dengan segitiga.
Kesimpulan
Jenis-jenis segitiga memiliki karakteristik dan sifat yang berbeda-beda. Memahaminya sangat penting untuk menyelesaikan masalah matematika dan memiliki aplikasi dalam berbagai bidang kehidupan nyata. Dengan menerapkan tips yang telah dibahas, Anda dapat meningkatkan kemampuan Anda dalam mengenali dan memahami segitiga.
Jenis-jenis Segitiga
Jenis-jenis segitiga memiliki peran penting dalam berbagai bidang, mulai dari matematika hingga teknik. Artikel ini telah mengeksplorasi berbagai jenis segitiga, sifat-sifatnya, dan penerapannya dalam kehidupan nyata. Dengan memahami jenis-jenis segitiga dan prinsip-prinsip yang mendasarinya, kita dapat menyelesaikan masalah yang melibatkan segitiga dengan lebih mudah dan efektif.
Ke depan, penelitian lebih lanjut tentang jenis-jenis segitiga dan aplikasinya dapat terus dilakukan. Hal ini akan memperluas pemahaman kita tentang geometri dan membuka kemungkinan baru untuk pemecahan masalah dan inovasi.
Youtube Video:
