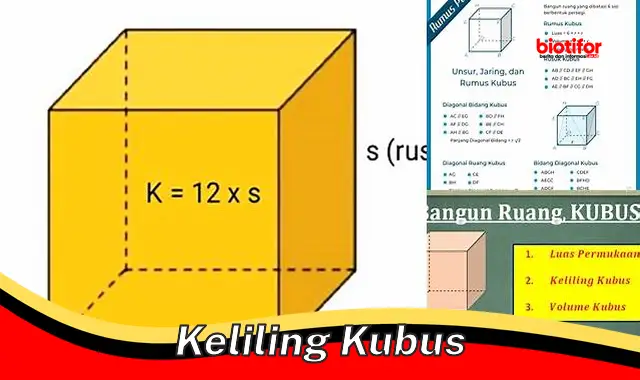
Keliling kubus adalah jumlah panjang semua rusuk kubus. Rumus untuk menghitung keliling kubus adalah 12 x rusuk. Misalnya, jika rusuk kubus adalah 5 cm, maka keliling kubusnya adalah 12 x 5 cm = 60 cm.
Keliling kubus penting untuk diketahui karena dapat digunakan untuk menghitung luas permukaan dan volume kubus. Selain itu, keliling kubus juga dapat digunakan untuk menyelesaikan berbagai masalah matematika, seperti mencari panjang diagonal kubus atau mencari panjang sisi kubus jika diketahui kelilingnya.
Dalam sejarah, keliling kubus telah digunakan oleh para matematikawan selama berabad-abad. Misalnya, Archimedes menggunakan keliling kubus untuk menghitung luas permukaan dan volume bola. Keliling kubus juga telah digunakan oleh para arsitek untuk merancang bangunan, seperti piramida di Mesir.
Keliling Kubus
Keliling kubus merupakan aspek penting dalam geometri. Berikut adalah 10 aspek penting terkait keliling kubus:
- Definisi: Jumlah panjang semua rusuk kubus.
- Rumus: 12 x rusuk.
- Satuan: Centimeter (cm), meter (m), atau satuan panjang lainnya.
- Manfaat: Menghitung luas permukaan dan volume kubus.
- Aplikasi: Menyelesaikan masalah matematika, merancang bangunan.
- Sejarah: Digunakan oleh Archimedes dan matematikawan lainnya.
- Jenis: Keliling kubus beraturan dan tidak beraturan.
- Sifat: Keliling kubus berbanding lurus dengan panjang rusuknya.
- Contoh: Kubus dengan rusuk 5 cm memiliki keliling 60 cm.
- Kaitan: Keliling kubus terkait dengan luas permukaan dan volumenya.
Keliling kubus memiliki peran penting dalam berbagai bidang, seperti matematika, fisika, dan arsitektur. Memahami aspek-aspek penting keliling kubus sangat bermanfaat untuk menyelesaikan masalah terkait bangun ruang dan merancang struktur yang efisien.
Definisi
Definisi keliling kubus sebagai jumlah panjang semua rusuk kubus sangat penting karena memberikan dasar untuk memahami dan menghitung keliling kubus. Tanpa definisi ini, tidak mungkin untuk menghitung keliling kubus karena tidak ada cara untuk menentukan panjang semua rusuknya. Selain itu, definisi ini juga memungkinkan kita untuk memahami hubungan antara keliling kubus dan panjang rusuknya, yaitu keliling kubus berbanding lurus dengan panjang rusuknya.
Dalam kehidupan nyata, definisi keliling kubus digunakan dalam berbagai aplikasi, seperti merancang dan membangun struktur, menghitung luas permukaan dan volume kubus, serta menyelesaikan masalah matematika. Misalnya, arsitek menggunakan definisi keliling kubus untuk menghitung jumlah bahan yang dibutuhkan untuk membangun sebuah kubus, dan insinyur menggunakannya untuk menghitung kekuatan dan stabilitas struktur kubus.
Dengan memahami definisi keliling kubus, kita dapat memperoleh wawasan yang lebih baik tentang sifat-sifat kubus dan menyelesaikan berbagai masalah yang berkaitan dengan bangun ruang ini.
Rumus
Rumus keliling kubus, yaitu 12 x rusuk, memiliki hubungan yang erat dengan keliling kubus. Rumus ini memberikan cara praktis untuk menghitung keliling kubus hanya dengan mengetahui panjang rusuknya. Pemahaman tentang rumus ini sangat penting untuk menyelesaikan berbagai masalah yang berkaitan dengan keliling kubus.
-
Menghitung Keliling Kubus
Rumus keliling kubus digunakan untuk menghitung keliling kubus dengan cepat dan mudah. Dengan hanya mengetahui panjang rusuknya, kita dapat langsung menghitung kelilingnya menggunakan rumus ini. Misalnya, jika rusuk kubus adalah 5 cm, maka keliling kubusnya adalah 12 x 5 cm = 60 cm.
Dengan memahami hubungan antara rumus keliling kubus dan keliling kubus, kita dapat menyelesaikan berbagai masalah matematika dan aplikasi praktis yang melibatkan kubus. Rumus ini menjadi alat penting dalam geometri untuk memahami dan menghitung keliling kubus secara efisien.
Satuan
Satuan keliling kubus sangat penting karena menunjukkan besaran dan skala keliling kubus. Satuan yang umum digunakan untuk keliling kubus adalah centimeter (cm) dan meter (m), tetapi satuan panjang lainnya juga dapat digunakan sesuai dengan kebutuhan dan konteks.
-
Penggunaan Satuan yang Tepat
Penggunaan satuan yang tepat sangat penting untuk memastikan akurasi dan konsistensi pengukuran keliling kubus. Misalnya, jika keliling kubus diukur dalam centimeter, maka satuan yang digunakan harus tetap centimeter sepanjang perhitungan dan pelaporan hasil.
Dengan memahami hubungan antara satuan dan keliling kubus, kita dapat mengukur dan membandingkan keliling kubus secara akurat dan efektif. Pemilihan satuan yang tepat juga akan memudahkan komunikasi dan pemahaman informasi terkait keliling kubus.
Manfaat
Keliling kubus memiliki peran penting dalam menghitung luas permukaan dan volume kubus. Luas permukaan kubus adalah jumlah luas semua sisi kubus, sedangkan volume kubus adalah ruang yang ditempati oleh kubus. Kedua besaran ini sangat penting dalam berbagai aplikasi, seperti desain arsitektur, teknik sipil, dan pengemasan.
Untuk menghitung luas permukaan kubus, kita dapat menggunakan rumus: 6 x (sisi x sisi). Dalam rumus ini, sisi adalah panjang salah satu sisi kubus. Dengan mengetahui keliling kubus, kita dapat dengan mudah menentukan panjang sisi kubus, yaitu dengan membagi keliling kubus dengan 12. Setelah mengetahui panjang sisi kubus, kita dapat menghitung luas permukaan kubus menggunakan rumus yang disebutkan sebelumnya.
Untuk menghitung volume kubus, kita dapat menggunakan rumus: (sisi x sisi x sisi). Sekali lagi, dengan mengetahui keliling kubus, kita dapat menentukan panjang sisi kubus dan kemudian menghitung volume kubus menggunakan rumus ini. Mengetahui keliling kubus sangat penting karena memungkinkan kita untuk menghitung luas permukaan dan volume kubus dengan mudah dan akurat.
Aplikasi
Keliling kubus memiliki aplikasi luas dalam menyelesaikan masalah matematika dan merancang bangunan. Dalam matematika, keliling kubus digunakan untuk menghitung luas permukaan dan volume kubus, yang merupakan aspek penting dalam geometri dan fisika. Misalnya, dalam menghitung volume sebuah kotak atau kubus, keliling kubus digunakan untuk menentukan panjang sisi kubus, yang kemudian digunakan untuk menghitung volumenya.
Dalam arsitektur dan teknik sipil, keliling kubus digunakan untuk merancang dan membangun struktur seperti rumah, jembatan, dan gedung. Misalnya, dalam merancang sebuah rumah, arsitek menggunakan keliling kubus untuk menentukan ukuran dan bentuk rumah, serta menghitung jumlah bahan bangunan yang dibutuhkan. Keliling kubus juga digunakan dalam merancang jembatan dan gedung untuk memastikan stabilitas dan kekuatan struktur.
Memahami hubungan antara keliling kubus dan aplikasi praktisnya sangat penting bagi siswa, insinyur, arsitek, dan siapa saja yang bekerja dengan geometri dan konstruksi. Dengan memahami konsep ini, kita dapat menyelesaikan masalah matematika yang kompleks, merancang bangunan yang efisien dan aman, serta berkontribusi pada kemajuan ilmu pengetahuan dan teknologi.
Sejarah
Sejarah penggunaan keliling kubus dapat ditelusuri hingga ke zaman Archimedes, seorang matematikawan Yunani yang hidup pada abad ke-3 SM. Archimedes dikenal karena kontribusinya yang signifikan dalam bidang geometri, termasuk penemuan rumus untuk menghitung keliling dan luas permukaan kubus. Rumus keliling kubus yang kita gunakan hingga saat ini, yaitu 12 x rusuk, pertama kali ditemukan oleh Archimedes.
Selain Archimedes, banyak matematikawan lain sepanjang sejarah yang juga menggunakan keliling kubus dalam penelitian dan penemuan mereka. Misalnya, Euclid, seorang matematikawan Yunani lainnya yang hidup pada abad ke-3 SM, menggunakan keliling kubus dalam bukunya “Elements” untuk menghitung volume kubus. Matematikawan India seperti Aryabhata dan Bhaskara juga menggunakan keliling kubus dalam karya mereka pada abad ke-5 dan ke-12 Masehi.
Pemahaman tentang sejarah penggunaan keliling kubus sangat penting karena memberikan konteks dan apresiasi yang lebih dalam terhadap konsep ini. Dengan mengetahui bahwa keliling kubus telah digunakan oleh matematikawan terkemuka selama berabad-abad, kita dapat lebih menghargai pentingnya dan kegunaannya dalam geometri dan bidang terkait lainnya.
Jenis
Dalam geometri, kubus dapat diklasifikasikan menjadi dua jenis berdasarkan bentuk dan ukuran rusuknya, yaitu kubus beraturan dan kubus tidak beraturan.
Kubus Beraturan
Kubus beraturan memiliki keenam rusuk yang sama panjang dan semua sudutnya siku-siku. Keliling kubus beraturan dihitung menggunakan rumus 12 x rusuk. Jenis kubus ini sering digunakan dalam matematika dan fisika karena sifat simetrisnya.
Kubus Tidak Beraturan
Kubus tidak beraturan memiliki rusuk yang tidak sama panjang dan sudut yang tidak siku-siku. Keliling kubus tidak beraturan dihitung dengan menjumlahkan panjang semua rusuknya. Jenis kubus ini lebih umum ditemukan dalam aplikasi dunia nyata, seperti pada bangunan dan kemasan.
Memahami perbedaan antara keliling kubus beraturan dan tidak beraturan sangat penting karena memiliki implikasi praktis dalam berbagai bidang. Misalnya, dalam arsitektur, jenis kubus yang digunakan akan mempengaruhi kekuatan dan stabilitas struktur bangunan. Dalam pengemasan, jenis kubus yang digunakan akan mempengaruhi efisiensi ruang dan biaya.
Sifat
Sifat keliling kubus yang berbanding lurus dengan panjang rusuknya memiliki peran penting dalam memahami dan menghitung keliling kubus. Sifat ini menyatakan bahwa semakin panjang rusuk kubus, semakin besar keliling kubusnya, dan sebaliknya. Hubungan ini memberikan implikasi praktis dalam berbagai aplikasi yang melibatkan kubus.
-
Kemudahan Perhitungan
Sifat ini memungkinkan kita untuk menghitung keliling kubus dengan mudah dan cepat. Dengan mengetahui panjang rusuk kubus, kita dapat langsung menghitung kelilingnya menggunakan rumus keliling kubus, yaitu 12 x rusuk. Sifat ini sangat berguna dalam menyelesaikan masalah matematika dan aplikasi praktis yang melibatkan kubus.
Dengan memahami sifat keliling kubus yang berbanding lurus dengan panjang rusuknya, kita dapat memperoleh wawasan yang lebih baik tentang sifat-sifat kubus dan menyelesaikan berbagai masalah yang berkaitan dengan bangun ruang ini.
Contoh
Contoh ini menyoroti hubungan antara keliling kubus dan panjang rusuknya. Dari contoh tersebut, kita dapat mengamati bahwa keliling kubus berbanding lurus dengan panjang rusuknya. Semakin panjang rusuk kubus, semakin besar keliling kubusnya. Hubungan ini sesuai dengan sifat keliling kubus yang telah dibahas sebelumnya.
Contoh ini sangat penting karena memberikan ilustrasi nyata tentang konsep keliling kubus. Dengan memahami contoh ini, kita dapat memperoleh pemahaman yang lebih baik tentang cara menghitung keliling kubus dan sifat-sifatnya. Selain itu, contoh ini juga dapat digunakan untuk menyelesaikan masalah matematika dan aplikasi praktis yang melibatkan kubus.
Sebagai contoh praktis, dalam arsitektur, memahami hubungan antara keliling kubus dan panjang rusuknya sangat penting untuk menentukan ukuran dan bentuk bangunan. Arsitek menggunakan rumus keliling kubus untuk menghitung jumlah bahan bangunan yang dibutuhkan dan memastikan stabilitas struktur bangunan.
Kaitan
Keliling kubus memiliki kaitan yang erat dengan luas permukaan dan volume kubus. Hubungan ini sangat penting dalam geometri dan memiliki aplikasi dalam berbagai bidang seperti arsitektur, teknik sipil, dan desain produk.
-
Menghitung Luas Permukaan
Keliling kubus dapat digunakan untuk menghitung luas permukaan kubus. Luas permukaan kubus adalah jumlah luas semua sisi kubus. Rumus untuk menghitung luas permukaan kubus adalah 6 x (sisi x sisi), di mana sisi adalah panjang salah satu sisi kubus. Keliling kubus dapat digunakan untuk menentukan panjang sisi kubus, yang kemudian digunakan untuk menghitung luas permukaan kubus.
-
Menghitung Volume
Keliling kubus juga dapat digunakan untuk menghitung volume kubus. Volume kubus adalah ruang yang ditempati oleh kubus. Rumus untuk menghitung volume kubus adalah (sisi x sisi x sisi), di mana sisi adalah panjang salah satu sisi kubus. Keliling kubus dapat digunakan untuk menentukan panjang sisi kubus, yang kemudian digunakan untuk menghitung volume kubus.
Memahami kaitan antara keliling kubus, luas permukaan, dan volume sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam arsitektur, kaitan ini digunakan untuk menentukan ukuran dan bentuk bangunan, serta menghitung jumlah bahan bangunan yang dibutuhkan. Dalam teknik sipil, kaitan ini digunakan untuk menghitung kekuatan dan stabilitas struktur seperti jembatan dan gedung. Dalam desain produk, kaitan ini digunakan untuk menentukan ukuran dan bentuk kemasan produk.
FAQ seputar Keliling Kubus
Berikut adalah beberapa pertanyaan umum dan jawabannya mengenai keliling kubus:
Pertanyaan 1: Apa yang dimaksud dengan keliling kubus?
Keliling kubus adalah jumlah panjang semua rusuk kubus.
Pertanyaan 2: Bagaimana cara menghitung keliling kubus?
Keliling kubus dapat dihitung dengan menggunakan rumus 12 x rusuk, di mana rusuk adalah panjang salah satu sisi kubus.
Pertanyaan 3: Apa satuan yang digunakan untuk menyatakan keliling kubus?
Satuan yang umum digunakan untuk menyatakan keliling kubus adalah centimeter (cm) atau meter (m).
Pertanyaan 4: Apa saja manfaat mengetahui keliling kubus?
Keliling kubus bermanfaat untuk menghitung luas permukaan dan volume kubus, serta menyelesaikan berbagai masalah matematika dan aplikasi praktis.
Pertanyaan 5: Apa saja jenis-jenis kubus berdasarkan kelilingnya?
Berdasarkan kelilingnya, kubus dapat dibedakan menjadi kubus beraturan dan kubus tidak beraturan.
Pertanyaan 6: Bagaimana cara menggunakan keliling kubus dalam kehidupan nyata?
Keliling kubus digunakan dalam berbagai aplikasi, seperti merancang bangunan, menghitung bahan bangunan, dan menyelesaikan masalah matematika.
Dengan memahami konsep keliling kubus dan jawaban atas pertanyaan-pertanyaan ini, kita dapat memperoleh wawasan yang lebih baik tentang sifat-sifat kubus dan menyelesaikan berbagai masalah yang berkaitan dengan bangun ruang ini.
Baca juga:
- Sifat-sifat Kubus
- Rumus-rumus Kubus
- Aplikasi Keliling Kubus
Tips Mengenai Keliling Kubus
Keliling kubus adalah aspek penting dalam geometri yang memiliki berbagai aplikasi dalam matematika dan kehidupan nyata. Berikut adalah beberapa tips untuk memahami dan menggunakan keliling kubus secara efektif:
Tip 1: Pahami Konsep Dasar
Keliling kubus adalah jumlah panjang semua rusuk kubus. Memahami definisi ini sangat penting untuk menghitung dan menggunakan keliling kubus dengan benar.
Tip 2: Gunakan Rumus yang Tepat
Rumus keliling kubus adalah 12 x rusuk. Gunakan rumus ini untuk menghitung keliling kubus secara akurat dan efisien.
Tip 3: Perhatikan Satuan
Keliling kubus biasanya dinyatakan dalam satuan centimeter (cm) atau meter (m). Pastikan untuk menggunakan satuan yang konsisten dalam perhitungan Anda.
Tip 4: Ketahui Aplikasi Praktis
Keliling kubus memiliki berbagai aplikasi praktis, seperti menghitung luas permukaan dan volume kubus, merancang bangunan, dan menyelesaikan masalah matematika. Pahami aplikasi ini untuk memanfaatkan keliling kubus secara maksimal.
Tip 5: Berlatihlah Secara Teratur
Latihan teratur akan membantu Anda menguasai konsep keliling kubus dan menerapkannya dengan efektif dalam berbagai situasi.
Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman dan keterampilan Anda dalam menggunakan keliling kubus untuk menyelesaikan masalah dan memperoleh wawasan tentang geometri.
Kesimpulan
Keliling kubus merupakan konsep penting dalam geometri yang memiliki berbagai aplikasi dalam kehidupan nyata. Dengan memahami konsep dasar, menggunakan rumus yang tepat, memperhatikan satuan, mengetahui aplikasi praktis, dan berlatih secara teratur, Anda dapat memanfaatkan keliling kubus untuk menyelesaikan masalah, memperoleh wawasan geometri, dan berkontribusi dalam berbagai bidang terkait.
Penutup
Keliling kubus merupakan konsep mendasar dalam geometri yang memiliki berbagai aplikasi dalam kehidupan nyata. Pemahaman tentang keliling kubus sangat penting dalam merancang bangunan, menghitung bahan bangunan, menyelesaikan masalah matematika, dan banyak lagi.
Dengan memahami sifat-sifat keliling kubus, rumus perhitungannya, serta kaitannya dengan luas permukaan dan volume kubus, kita dapat memanfaatkan konsep ini secara efektif untuk memecahkan masalah dan memperoleh wawasan yang lebih baik tentang geometri. Keliling kubus akan terus menjadi aspek penting dalam matematika dan aplikasi praktis di masa depan.
Youtube Video:
