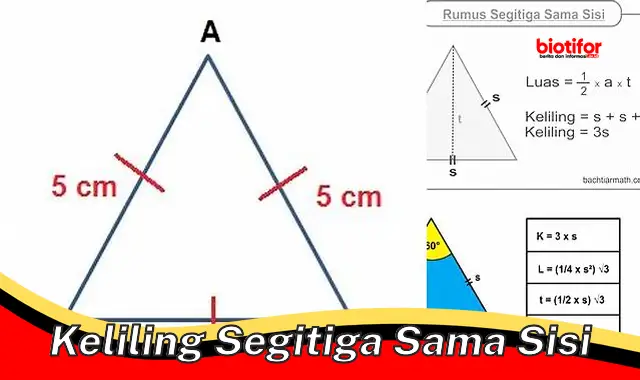
Keliling segitiga sama sisi adalah jumlah panjang ketiga sisinya. Karena ketiga sisi segitiga sama sisi sama panjang, maka kelilingnya dapat dihitung dengan mengalikan panjang satu sisi dengan 3. Misalnya, jika panjang sisi segitiga sama sisi adalah 5 cm, maka kelilingnya adalah 5 cm x 3 = 15 cm.
Keliling segitiga sama sisi penting dalam berbagai bidang, seperti arsitektur, teknik, dan matematika. Dalam arsitektur, keliling segitiga sama sisi digunakan untuk menghitung luas permukaan bangunan. Dalam teknik, keliling segitiga sama sisi digunakan untuk menghitung panjang kabel atau pipa yang dibutuhkan untuk suatu proyek. Dalam matematika, keliling segitiga sama sisi digunakan untuk mempelajari sifat-sifat segitiga.
Selain itu, keliling segitiga sama sisi juga memiliki sejarah yang panjang. Konsep keliling segitiga sama sisi pertama kali ditemukan oleh matematikawan Yunani kuno, Pythagoras. Pythagoras menggunakan keliling segitiga sama sisi untuk mengembangkan teorema Pythagoras, yang merupakan salah satu teorema terpenting dalam matematika.
Keliling Segitiga Sama Sisi
Keliling segitiga sama sisi merupakan aspek penting dalam memahami geometri dan memiliki beberapa dimensi yang saling terkait, yaitu:
- Panjang Sisi
- Jumlah Sisi
- Rumus Keliling
- Satuan Keliling
- Jenis Segitiga
- Sifat Keliling
- Aplikasi Keliling
- Sejarah Keliling
Kedelapan aspek ini saling terkait dan memberikan pemahaman yang komprehensif tentang keliling segitiga sama sisi. Misalnya, panjang sisi memengaruhi keliling, begitu juga jumlah sisi dan jenis segitiga. Rumus keliling memberikan cara praktis untuk menghitung keliling, sementara satuan keliling memastikan konsistensi pengukuran. Sifat keliling, seperti tidak berubah jika segitiga diputar atau dicerminkan, memberikan wawasan penting tentang geometri. Terakhir, aplikasi keliling dalam berbagai bidang seperti arsitektur dan teknik menyoroti relevansinya dalam dunia nyata. Memahami aspek-aspek ini sangat penting untuk menguasai konsep keliling segitiga sama sisi.
Panjang Sisi
Panjang sisi merupakan komponen krusial dari keliling segitiga sama sisi. Keliling segitiga sama sisi adalah jumlah panjang ketiga sisinya, sehingga panjang sisi berbanding lurus dengan keliling. Artinya, semakin panjang sisi segitiga sama sisi, semakin besar pula kelilingnya.
Hubungan antara panjang sisi dan keliling segitiga sama sisi sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam arsitektur, panjang sisi segitiga sama sisi menentukan keliling suatu bangunan. Dalam teknik, panjang sisi segitiga sama sisi menentukan panjang kabel atau pipa yang dibutuhkan untuk suatu proyek. Dalam matematika, panjang sisi segitiga sama sisi digunakan untuk menghitung luas dan tinggi segitiga.
Memahami hubungan antara panjang sisi dan keliling segitiga sama sisi sangat penting untuk berbagai bidang. Hal ini memungkinkan kita untuk menghitung keliling segitiga sama sisi secara akurat, merancang bangunan dan struktur yang efisien, serta memecahkan masalah matematika yang kompleks.
Jumlah Sisi
Jumlah sisi merupakan komponen penting dari keliling segitiga sama sisi. Keliling segitiga sama sisi adalah jumlah panjang ketiga sisinya, sehingga jumlah sisi berbanding lurus dengan keliling. Artinya, semakin banyak sisi segitiga sama sisi, semakin besar pula kelilingnya.
Hubungan antara jumlah sisi dan keliling segitiga sama sisi sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam arsitektur, jumlah sisi segitiga sama sisi menentukan jumlah sisi suatu bangunan. Dalam teknik, jumlah sisi segitiga sama sisi menentukan jumlah sisi suatu benda yang akan dibuat. Dalam matematika, jumlah sisi segitiga sama sisi digunakan untuk menghitung luas dan tinggi segitiga.
Memahami hubungan antara jumlah sisi dan keliling segitiga sama sisi sangat penting untuk berbagai bidang. Hal ini memungkinkan kita untuk menghitung keliling segitiga sama sisi secara akurat, merancang bangunan dan struktur yang efisien, serta memecahkan masalah matematika yang kompleks.
Rumus Keliling
Rumus keliling segitiga sama sisi sangat penting untuk menghitung keliling segitiga sama sisi secara akurat. Rumus keliling segitiga sama sisi adalah K = 3s, di mana K adalah keliling dan s adalah panjang sisi segitiga sama sisi. Rumus ini menunjukkan bahwa keliling segitiga sama sisi adalah tiga kali panjang sisinya.
Memahami rumus keliling segitiga sama sisi sangat penting dalam berbagai bidang. Misalnya, dalam arsitektur, rumus keliling segitiga sama sisi digunakan untuk menghitung keliling bangunan yang berbentuk segitiga sama sisi. Dalam teknik, rumus keliling segitiga sama sisi digunakan untuk menghitung panjang pagar yang mengelilingi taman yang berbentuk segitiga sama sisi. Dalam matematika, rumus keliling segitiga sama sisi digunakan untuk menghitung keliling segitiga sama sisi dalam soal-soal matematika.
Dengan memahami rumus keliling segitiga sama sisi, kita dapat menghitung keliling segitiga sama sisi dengan cepat dan mudah. Hal ini sangat penting untuk berbagai aplikasi praktis, seperti merancang bangunan, membuat pagar, dan menyelesaikan soal-soal matematika.
Satuan Keliling
Satuan keliling merupakan komponen penting dalam pengukuran keliling segitiga sama sisi. Satuan keliling adalah besaran yang digunakan untuk menyatakan panjang keliling, seperti sentimeter (cm), meter (m), atau kilometer (km). Pemilihan satuan keliling yang tepat sangat penting untuk memastikan konsistensi dan akurasi pengukuran.
Dalam konteks keliling segitiga sama sisi, satuan keliling digunakan untuk menyatakan panjang total ketiga sisinya. Misalnya, jika panjang sisi segitiga sama sisi adalah 10 cm, maka kelilingnya adalah 30 cm. Satuan keliling yang digunakan dalam kasus ini adalah cm, yang menunjukkan bahwa keliling segitiga sama sisi tersebut adalah 30 sentimeter.
Memahami hubungan antara satuan keliling dan keliling segitiga sama sisi sangat penting untuk berbagai aplikasi praktis. Misalnya, dalam arsitektur, satuan keliling digunakan untuk menentukan keliling bangunan yang berbentuk segitiga sama sisi. Dalam teknik, satuan keliling digunakan untuk menghitung panjang pagar yang mengelilingi taman yang berbentuk segitiga sama sisi. Dalam matematika, satuan keliling digunakan untuk menyelesaikan soal-soal matematika yang melibatkan keliling segitiga sama sisi.
Jenis Segitiga
Jenis segitiga memiliki kaitan erat dengan keliling segitiga sama sisi. Segitiga sama sisi adalah segitiga yang memiliki tiga sisi sama panjang. Oleh karena itu, keliling segitiga sama sisi dipengaruhi oleh panjang sisi segitiga tersebut.
Sebagai contoh, jika kita memiliki segitiga sama sisi dengan panjang sisi 10 cm, maka keliling segitiga tersebut adalah 3 x 10 cm = 30 cm. Hal ini menunjukkan bahwa jenis segitiga, yaitu segitiga sama sisi, menentukan cara menghitung kelilingnya, yaitu dengan mengalikan panjang sisi dengan 3.
Memahami hubungan antara jenis segitiga dan keliling segitiga sama sisi sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam arsitektur, jenis segitiga digunakan untuk menentukan keliling bangunan yang berbentuk segitiga sama sisi. Dalam teknik, jenis segitiga digunakan untuk menghitung panjang pagar yang mengelilingi taman yang berbentuk segitiga sama sisi. Dalam matematika, jenis segitiga digunakan untuk menyelesaikan soal-soal matematika yang melibatkan keliling segitiga sama sisi.
Sifat Keliling
Sifat keliling sangat penting dalam memahami keliling segitiga sama sisi. Sifat keliling adalah karakteristik yang dimiliki oleh keliling segitiga sama sisi, yang membedakannya dari bangun datar lainnya.
-
Tidak Berubah Jika Diputar atau Dicerminkan
Keliling segitiga sama sisi tidak berubah jika segitiga tersebut diputar atau dicerminkan. Hal ini karena ketiga sisi segitiga sama sisi sama panjang, sehingga rotasi atau pencerminan tidak memengaruhi panjang total ketiga sisinya.
-
Selalu Kelipatan Tiga Panjang Sisi
Keliling segitiga sama sisi selalu merupakan kelipatan tiga dari panjang sisinya. Hal ini karena keliling segitiga sama sisi dihitung dengan mengalikan panjang sisi dengan 3.
-
Lebih Besar dari Luas Segitiga Sama Sisi
Keliling segitiga sama sisi selalu lebih besar dari luas segitiga sama sisi. Hal ini karena keliling segitiga sama sisi adalah jumlah panjang ketiga sisinya, sedangkan luas segitiga sama sisi adalah setengah dari hasil kali alas dan tinggi segitiga.
Sifat-sifat keliling ini sangat penting dalam memahami dan menyelesaikan masalah yang melibatkan keliling segitiga sama sisi. Dengan memahami sifat-sifat ini, kita dapat menghitung keliling segitiga sama sisi dengan cepat dan mudah, serta memecahkan masalah matematika yang kompleks.
Aplikasi Keliling
Aplikasi keliling sangat penting dalam kehidupan nyata. Dalam konteks keliling segitiga sama sisi, aplikasi keliling sangat krusial karena digunakan untuk menghitung panjang total ketiga sisi segitiga sama sisi. Keliling segitiga sama sisi digunakan dalam berbagai bidang, seperti arsitektur, teknik, dan matematika.
Dalam arsitektur, keliling segitiga sama sisi digunakan untuk menghitung keliling bangunan yang berbentuk segitiga sama sisi. Keliling bangunan sangat penting untuk menentukan jumlah bahan bangunan yang dibutuhkan, seperti batu bata, semen, dan cat. Selain itu, keliling bangunan juga digunakan untuk menghitung biaya pembangunan.
Dalam teknik, keliling segitiga sama sisi digunakan untuk menghitung panjang pagar yang mengelilingi taman yang berbentuk segitiga sama sisi. Keliling taman sangat penting untuk menentukan jumlah pagar yang dibutuhkan dan biaya pemasangan pagar. Selain itu, keliling taman juga digunakan untuk menghitung luas taman.
Dalam matematika, keliling segitiga sama sisi digunakan untuk menyelesaikan soal-soal matematika yang melibatkan keliling segitiga sama sisi. Keliling segitiga sama sisi sangat penting untuk memahami sifat-sifat segitiga sama sisi dan menyelesaikan masalah matematika yang kompleks.
Memahami aplikasi keliling segitiga sama sisi sangat penting untuk berbagai bidang. Dengan memahami aplikasi keliling segitiga sama sisi, kita dapat menghitung keliling segitiga sama sisi dengan cepat dan mudah, serta menyelesaikan masalah dalam kehidupan nyata yang melibatkan keliling segitiga sama sisi.
Sejarah Keliling
Sejarah keliling erat kaitannya dengan perkembangan matematika dan geometri. Konsep keliling telah dikenal sejak zaman dahulu dan digunakan dalam berbagai bidang seperti arsitektur, teknik, dan pertanian.
-
Zaman Babilonia
Konsep keliling pertama kali ditemukan oleh bangsa Babilonia sekitar tahun 1900-1600 SM. Mereka menggunakan rumus keliling lingkaran yang berbunyi K = d, di mana K adalah keliling, d adalah diameter, dan adalah konstanta sekitar 3,14.
-
Zaman Yunani
Matematikawan Yunani seperti Thales dan Pythagoras mengembangkan konsep keliling lebih lanjut. Thales menggunakan keliling untuk menghitung tinggi bangunan, sedangkan Pythagoras menggunakan keliling untuk membuktikan teorema Pythagoras.
-
Zaman Romawi
Bangsa Romawi menggunakan konsep keliling untuk membangun jalan, jembatan, dan bangunan. Mereka juga mengembangkan rumus keliling untuk bangun datar seperti persegi, persegi panjang, dan segitiga.
-
Zaman Islam
Matematikawan Islam seperti Al-Khawarizmi dan Al-Biruni mengembangkan konsep keliling lebih lanjut. Mereka memperkenalkan rumus keliling untuk bangun datar yang lebih kompleks, seperti lingkaran dan elips.
Konsep keliling terus berkembang seiring dengan perkembangan matematika dan geometri. Saat ini, konsep keliling digunakan dalam berbagai bidang, termasuk arsitektur, teknik, dan matematika.
FAQ Keliling Segitiga Sama Sisi
Berikut beberapa pertanyaan umum dan jawabannya terkait keliling segitiga sama sisi:
Pertanyaan 1: Bagaimana cara menghitung keliling segitiga sama sisi?
Jawaban: Keliling segitiga sama sisi dihitung dengan mengalikan panjang sisi segitiga tersebut dengan 3.
Pertanyaan 2: Apa satuan yang biasa digunakan untuk menyatakan keliling segitiga sama sisi?
Jawaban: Satuan yang biasa digunakan untuk menyatakan keliling segitiga sama sisi adalah cm (sentimeter), m (meter), atau km (kilometer), tergantung pada konteks penggunaannya.
Pertanyaan 3: Apakah keliling segitiga sama sisi selalu lebih besar dari luasnya?
Jawaban: Ya, keliling segitiga sama sisi selalu lebih besar dari luasnya karena keliling adalah jumlah panjang sisi-sisinya, sedangkan luas adalah setengah dari hasil kali alas dan tinggi segitiga.
Pertanyaan 4: Di bidang apa saja keliling segitiga sama sisi digunakan?
Jawaban: Keliling segitiga sama sisi digunakan dalam berbagai bidang, seperti arsitektur, teknik, dan matematika.
Pertanyaan 5: Bagaimana cara menerapkan konsep keliling segitiga sama sisi dalam kehidupan nyata?
Jawaban: Konsep keliling segitiga sama sisi dapat diterapkan dalam kehidupan nyata, misalnya untuk menghitung panjang pagar yang mengelilingi taman berbentuk segitiga sama sisi atau untuk menghitung jumlah bahan bangunan yang dibutuhkan untuk membangun rumah berbentuk segitiga sama sisi.
Pertanyaan 6: Apa manfaat mempelajari keliling segitiga sama sisi?
Jawaban: Mempelajari keliling segitiga sama sisi bermanfaat karena dapat membantu kita memecahkan masalah dalam berbagai bidang, seperti arsitektur, teknik, dan matematika.
Dengan memahami konsep dan aplikasi keliling segitiga sama sisi, kita dapat menyelesaikan masalah yang melibatkan bangun datar tersebut dengan lebih mudah dan akurat.
Lanjut ke bagian selanjutnya: Sejarah Keliling
Tips Menghitung Keliling Segitiga Sama Sisi
Keliling segitiga sama sisi adalah jumlah panjang ketiga sisinya yang sama panjang. Berikut beberapa tips untuk menghitung keliling segitiga sama sisi dengan mudah dan akurat:
Tip 1: Hafalkan Rumus Keliling Segitiga Sama Sisi
Rumus keliling segitiga sama sisi adalah K = 3s, di mana K adalah keliling dan s adalah panjang sisi segitiga sama sisi. Dengan menghafal rumus ini, Anda dapat dengan mudah menghitung keliling segitiga sama sisi tanpa harus mengingat cara menghitungnya dari awal.
Tip 2: Pastikan Satuan Panjang Konsisten
Saat menghitung keliling segitiga sama sisi, pastikan satuan panjang yang digunakan untuk mengukur sisi segitiga sama sisi konsisten. Misalnya, jika Anda mengukur sisi segitiga sama sisi dalam sentimeter, maka hasil kelilingnya juga harus dalam sentimeter.
Tip 3: Gambarlah Segitiga Sama Sisi
Jika Anda kesulitan memvisualisasikan segitiga sama sisi, cobalah untuk menggambar segitiga sama sisi terlebih dahulu. Dengan menggambar segitiga sama sisi, Anda dapat melihat dengan jelas ketiga sisi yang sama panjang dan menghitung kelilingnya dengan lebih mudah.
Tip 4: Gunakan Kalkulator
Jika Anda tidak ingin menghitung keliling segitiga sama sisi secara manual, Anda dapat menggunakan kalkulator. Dengan menggunakan kalkulator, Anda dapat menghitung keliling segitiga sama sisi dengan cepat dan akurat.
Tip 5: Periksa Kembali Hasil Anda
Setelah menghitung keliling segitiga sama sisi, periksa kembali hasil Anda untuk memastikan bahwa hasilnya masuk akal. Anda dapat memeriksa kembali hasil Anda dengan menghitung ulang keliling segitiga sama sisi menggunakan metode yang berbeda atau dengan meminta bantuan orang lain.
Dengan mengikuti tips ini, Anda dapat menghitung keliling segitiga sama sisi dengan mudah dan akurat. Keliling segitiga sama sisi sangat penting dalam berbagai bidang, seperti arsitektur, teknik, dan matematika. Dengan menguasai cara menghitung keliling segitiga sama sisi, Anda dapat menyelesaikan masalah yang melibatkan bangun datar tersebut dengan lebih mudah dan percaya diri.
Kesimpulan
Keliling segitiga sama sisi merupakan aspek penting dalam geometri yang memiliki berbagai aplikasi dalam kehidupan nyata. Konsep keliling segitiga sama sisi yang mencakup panjang sisi, jumlah sisi, rumus keliling, satuan keliling, jenis segitiga, sifat keliling, aplikasi keliling, dan sejarah keliling, memberikan pemahaman yang komprehensif tentang bangun datar ini. Memahami keliling segitiga sama sisi sangat penting untuk menyelesaikan masalah dalam berbagai bidang, seperti arsitektur, teknik, dan matematika.
Dengan menguasai konsep keliling segitiga sama sisi, kita dapat memahami dan menyelesaikan masalah yang melibatkan bangun datar tersebut dengan lebih mudah dan akurat. Keliling segitiga sama sisi akan terus menjadi topik penting dalam geometri dan akan terus memainkan peran penting dalam berbagai bidang kehidupan.
Youtube Video:
