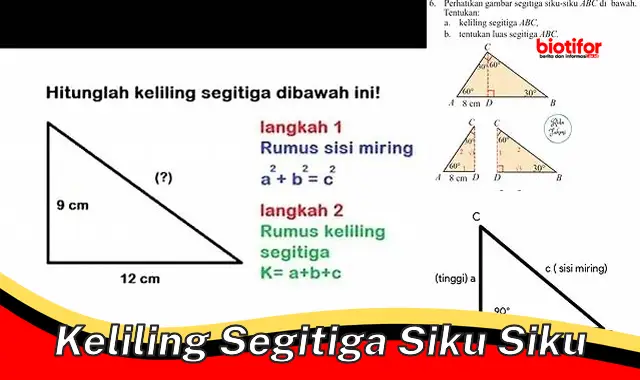
Keliling segitiga siku-siku adalah jumlah dari panjang ketiga sisinya. Dalam segitiga siku-siku, terdapat tiga sisi, yaitu sisi miring (sisi terpanjang yang berhadapan dengan sudut siku-siku), sisi siku-siku (dua sisi yang membentuk sudut siku-siku), dan sisi alas (sisi yang terletak di hadapan sudut yang bukan siku-siku). Rumus untuk mencari keliling segitiga siku-siku adalah:
K = s + s + m
Dengan K adalah keliling, s adalah panjang sisi siku-siku, dan m adalah panjang sisi miring.
Keliling segitiga siku-siku memiliki beberapa sifat penting. Pertama, keliling segitiga siku-siku selalu lebih besar dari panjang sisi terpanjangnya. Kedua, keliling segitiga siku-siku tidak berubah jika salah satu sudutnya diubah, selama sisi-sisinya tetap sama.
Keliling segitiga siku-siku memiliki berbagai aplikasi dalam kehidupan nyata, seperti dalam bidang arsitektur, teknik, dan desain. Dalam arsitektur, keliling segitiga siku-siku digunakan untuk menghitung panjang bahan yang dibutuhkan untuk membangun atap atau dinding. Dalam teknik, keliling segitiga siku-siku digunakan untuk menghitung gaya yang bekerja pada struktur.
Keliling segitiga siku-siku juga memiliki sejarah yang panjang. Rumus untuk mencari keliling segitiga siku-siku telah dikenal sejak zaman kuno. Bangsa Babilonia menggunakan rumus ini untuk menghitung keliling piramida dan bangunan lainnya. Bangsa Yunani juga menggunakan rumus ini dalam studi geometri mereka.
keliling segitiga siku siku
Keliling segitiga siku-siku merupakan aspek penting dalam geometri. Berikut adalah 9 aspek penting yang berkaitan dengan keliling segitiga siku-siku:
- Definisi
- Rumus
- Sifat
- Aplikasi
- Sejarah
- Sisi miring
- Sisi siku-siku
- Sisi alas
- Sudut siku-siku
Aspek-aspek ini saling terkait dan membentuk pemahaman yang komprehensif tentang keliling segitiga siku-siku. Misalnya, rumus keliling segitiga siku-siku dapat digunakan untuk menghitung panjang sisi miring, sisi siku-siku, atau sisi alas. Sifat keliling segitiga siku-siku dapat digunakan untuk menyelesaikan berbagai masalah geometri. Aplikasi keliling segitiga siku-siku dapat ditemukan dalam berbagai bidang, seperti arsitektur, teknik, dan desain.
Definisi
Definisi keliling segitiga siku-siku sangat penting untuk memahami konsep ini. Keliling segitiga siku-siku didefinisikan sebagai jumlah panjang ketiga sisinya. Definisi ini memberikan dasar untuk memahami sifat-sifat dan aplikasi keliling segitiga siku-siku.
-
Panjang Sisi
Definisi keliling segitiga siku-siku menekankan pentingnya panjang sisi-sisinya. Ketiga sisi segitiga siku-siku, yaitu sisi miring, sisi siku-siku, dan sisi alas, memiliki panjang tertentu yang menentukan kelilingnya.
-
Jumlah Sisi
Definisi keliling segitiga siku-siku juga menyoroti bahwa kelilingnya adalah jumlah panjang ketiga sisinya. Artinya, untuk menghitung keliling segitiga siku-siku, kita perlu menjumlahkan panjang sisi miring, sisi siku-siku, dan sisi alasnya.
-
Bentuk Segitiga
Definisi keliling segitiga siku-siku hanya berlaku untuk segitiga siku-siku. Artinya, definisi ini tidak dapat diterapkan pada jenis segitiga lainnya, seperti segitiga sama sisi atau segitiga sama kaki.
-
Satuan Panjang
Definisi keliling segitiga siku-siku juga terkait dengan satuan panjang. Keliling segitiga siku-siku dinyatakan dalam satuan panjang tertentu, seperti sentimeter, meter, atau kilometer.
Dengan memahami definisi keliling segitiga siku-siku, kita dapat memperoleh dasar yang kuat untuk mengeksplorasi sifat-sifat dan aplikasinya lebih lanjut.
Rumus
Rumus keliling segitiga siku-siku merupakan komponen penting dalam memahami dan menghitung keliling segitiga siku-siku. Rumus ini memberikan hubungan langsung antara panjang sisi-sisi segitiga siku-siku dan kelilingnya.
Rumus keliling segitiga siku-siku adalah:
K = s + s + m
di mana:
K adalah keliling segitiga siku-siku
s adalah panjang sisi siku-siku
m adalah panjang sisi miring
Rumus ini menunjukkan bahwa keliling segitiga siku-siku adalah jumlah dari panjang ketiga sisinya, yaitu dua sisi siku-siku dan sisi miring. Dengan menggunakan rumus ini, kita dapat menghitung keliling segitiga siku-siku jika kita mengetahui panjang sisi-sisinya.
Dalam praktiknya, rumus keliling segitiga siku-siku sangat berguna dalam berbagai bidang, seperti:
– Arsitektur dan konstruksi: Untuk menghitung keliling bangunan atau struktur yang berbentuk segitiga siku-siku.
– Teknik sipil: Untuk menghitung keliling jembatan, bendungan, atau struktur teknik lainnya yang berbentuk segitiga siku-siku.
– Desain dan kerajinan: Untuk menghitung keliling benda-benda yang berbentuk segitiga siku-siku, seperti bingkai foto, papan nama, atau pola jahit.
Memahami rumus keliling segitiga siku-siku sangat penting untuk menyelesaikan masalah geometri dan aplikasi praktis lainnya. Dengan menggunakan rumus ini, kita dapat menentukan keliling segitiga siku-siku secara akurat dan efisien.
Sifat
Sifat keliling segitiga siku-siku memainkan peran penting dalam memahami dan menerapkan konsep ini. Sifat-sifat ini menjelaskan karakteristik unik dari keliling segitiga siku-siku dan kaitannya dengan sisi-sisinya.
Salah satu sifat penting dari keliling segitiga siku-siku adalah selalu lebih besar dari panjang sisi terpanjangnya. Sifat ini berlaku untuk semua segitiga siku-siku, tanpa memandang ukuran atau bentuknya. Sifat ini memiliki implikasi praktis dalam berbagai bidang, seperti:
– Arsitektur: Untuk memastikan bahwa struktur yang berbentuk segitiga siku-siku memiliki kekuatan dan stabilitas yang cukup.
– Teknik sipil: Untuk merancang jembatan dan struktur lainnya agar dapat menahan beban dan gaya yang bekerja padanya.
Sifat penting lainnya dari keliling segitiga siku-siku adalah tidak berubah jika salah satu sudutnya diubah, selama sisi-sisinya tetap sama. Sifat ini menunjukkan bahwa keliling segitiga siku-siku ditentukan oleh panjang sisi-sisinya, bukan oleh ukuran sudut-sudutnya. Sifat ini berguna dalam:
– Matematika: Untuk menyelesaikan masalah geometri dan membuktikan teorema.
– Desain: Untuk membuat pola dan bentuk yang simetris dan harmonis.
Memahami sifat-sifat keliling segitiga siku-siku sangat penting untuk menggunakan konsep ini secara efektif dalam berbagai aplikasi praktis. Sifat-sifat ini memberikan wawasan berharga tentang perilaku dan karakteristik keliling segitiga siku-siku, sehingga memungkinkan kita untuk membuat keputusan yang tepat dan menyelesaikan masalah secara efisien.
Aplikasi
Keliling segitiga siku-siku memiliki banyak aplikasi dalam berbagai bidang kehidupan. Salah satu aplikasi yang penting adalah dalam bidang arsitektur. Dalam arsitektur, keliling segitiga siku-siku digunakan untuk menghitung kebutuhan material dan biaya pembangunan struktur berbentuk segitiga siku-siku, seperti atap, dinding, dan rangka bangunan. Ketepatan dalam menghitung keliling segitiga siku-siku sangat penting untuk memastikan kekuatan dan stabilitas struktur bangunan.
Aplikasi lainnya dari keliling segitiga siku-siku adalah dalam bidang teknik sipil. Dalam teknik sipil, keliling segitiga siku-siku digunakan untuk menghitung beban dan gaya yang bekerja pada struktur seperti jembatan, bendungan, dan menara. Dengan mengetahui keliling segitiga siku-siku, para insinyur dapat merancang struktur yang aman dan tahan lama.
Selain itu, keliling segitiga siku-siku juga digunakan dalam bidang desain dan kerajinan. Dalam desain, keliling segitiga siku-siku digunakan untuk menciptakan bentuk dan pola yang harmonis dan estetis. Dalam kerajinan, keliling segitiga siku-siku digunakan untuk menentukan ukuran dan bentuk benda yang akan dibuat, seperti bingkai foto, papan nama, dan pola jahit.
Dengan demikian, keliling segitiga siku-siku memiliki peran yang penting dalam berbagai aplikasi praktis. Kemampuan untuk menghitung dan memahami keliling segitiga siku-siku sangat penting bagi arsitek, insinyur, dan desainer untuk menciptakan struktur dan benda yang kuat, aman, dan indah.
Sejarah
Sejarah memiliki hubungan yang erat dengan konsep keliling segitiga siku siku. Sejak zaman dahulu, manusia telah menggunakan segitiga siku siku untuk berbagai keperluan, seperti dalam bidang arsitektur, teknik, dan navigasi. Pemahaman tentang keliling segitiga siku siku sangat penting untuk memastikan keakuratan dan efisiensi dalam berbagai aplikasi ini.
Salah satu contoh nyata dari pentingnya sejarah dalam memahami keliling segitiga siku siku adalah dalam pembangunan piramida di Mesir kuno. Bangsa Mesir menggunakan pengetahuan mereka tentang keliling segitiga siku siku untuk membangun struktur piramida yang presisi dan kokoh. Mereka menggunakan tali yang dibagi menjadi 12 bagian yang sama untuk membentuk segitiga siku siku, yang kemudian digunakan untuk menentukan sudut dan dimensi piramida.
Selain itu, sejarah juga memberikan wawasan tentang perkembangan rumus keliling segitiga siku siku. Rumus yang kita gunakan saat ini, yaitu K = s + s + m, pertama kali dikembangkan oleh matematikawan Yunani Pythagoras pada abad ke-6 SM. Teorema Pythagoras, yang menghubungkan keliling segitiga siku siku dengan panjang sisi-sisinya, telah menjadi dasar penting dalam geometri dan trigonometri selama berabad-abad.
Dengan memahami sejarah keliling segitiga siku siku, kita dapat menghargai pentingnya konsep ini dan bagaimana konsep ini telah digunakan sepanjang waktu. Pengetahuan ini tidak hanya memperkaya pemahaman kita tentang matematika, tetapi juga memungkinkan kita untuk mengapresiasi pencapaian ilmiah dan teknik dari peradaban masa lalu.
Sisi Miring
Sisi miring dalam segitiga siku-siku memiliki hubungan yang erat dengan keliling segitiga siku-siku. Sisi miring adalah sisi terpanjang pada segitiga siku-siku, dan panjangnya mempengaruhi nilai keliling segitiga siku-siku secara keseluruhan.
-
Definisi
Sisi miring pada segitiga siku siku adalah sisi yang terletak di hadapan sudut siku-siku. Sisi ini selalu merupakan sisi terpanjang pada segitiga siku siku.
-
Pengaruh pada Keliling
Panjang sisi miring berdampak langsung pada keliling segitiga siku-siku. Keliling segitiga siku-siku dihitung dengan menjumlahkan panjang ketiga sisinya, termasuk sisi miring. Semakin panjang sisi miring, semakin besar keliling segitiga siku-siku.
-
Rumus Keliling
Rumus keliling segitiga siku-siku melibatkan panjang sisi miring. Rumus keliling segitiga siku-siku adalah: K = s + s + m, di mana K adalah keliling, s adalah panjang sisi siku-siku, dan m adalah panjang sisi miring.
-
Aplikasi Praktis
Memahami hubungan antara sisi miring dan keliling segitiga siku-siku memiliki aplikasi praktis dalam berbagai bidang, seperti arsitektur dan teknik. Misalnya, dalam arsitektur, mengetahui keliling segitiga siku-siku penting untuk menghitung kebutuhan material dan biaya pembangunan struktur berbentuk segitiga siku-siku, seperti atap dan dinding.
Kesimpulannya, sisi miring memainkan peran penting dalam menentukan keliling segitiga siku-siku. Panjang sisi miring berdampak langsung pada nilai keliling, dan rumus keliling segitiga siku-siku memperhitungkan panjang sisi miring. Memahami hubungan ini sangat penting untuk berbagai aplikasi praktis, seperti dalam arsitektur dan teknik.
Sisi Siku-siku
Sisi siku-siku merupakan komponen penting dalam keliling segitiga siku-siku. Keliling segitiga siku-siku dihitung dengan menjumlahkan panjang ketiga sisinya, termasuk dua sisi siku-siku. Dengan demikian, panjang sisi siku-siku berdampak langsung pada nilai keliling segitiga siku-siku.
Sebagai contoh, perhatikan dua segitiga siku-siku dengan sisi siku-siku yang berbeda. Jika segitiga pertama memiliki sisi siku-siku sepanjang 5 cm dan 12 cm, maka kelilingnya adalah 5 cm + 12 cm + 13 cm = 30 cm. Sementara itu, jika segitiga kedua memiliki sisi siku-siku sepanjang 8 cm dan 15 cm, maka kelilingnya adalah 8 cm + 15 cm + 17 cm = 40 cm. Dari contoh ini, terlihat jelas bahwa perbedaan panjang sisi siku-siku menyebabkan perbedaan nilai keliling segitiga siku-siku.
Memahami hubungan antara sisi siku-siku dan keliling segitiga siku-siku sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam arsitektur, menghitung keliling segitiga siku-siku penting untuk menentukan kebutuhan material dan biaya pembangunan struktur berbentuk segitiga siku-siku, seperti atap dan dinding. Selain itu, dalam teknik sipil, keliling segitiga siku-siku digunakan untuk menghitung beban dan gaya yang bekerja pada struktur seperti jembatan dan menara.
Kesimpulannya, sisi siku-siku memiliki hubungan yang erat dengan keliling segitiga siku-siku. Panjang sisi siku-siku berdampak langsung pada nilai keliling, dan rumus keliling segitiga siku-siku memperhitungkan panjang sisi siku-siku. Memahami hubungan ini sangat penting untuk berbagai aplikasi praktis, seperti dalam arsitektur dan teknik.
Sisi Alas
Sisi alas merupakan salah satu dari tiga sisi yang membentuk segitiga siku-siku. Sisi ini terletak di hadapan sudut yang bukan siku-siku, atau dengan kata lain, sisi alas adalah sisi yang menghubungkan kedua sisi siku-siku. Pemahaman tentang sisi alas sangat penting dalam menghitung keliling segitiga siku-siku.
-
Pengaruh pada Keliling
Sisi alas berdampak langsung pada keliling segitiga siku-siku. Keliling segitiga siku-siku dihitung dengan menjumlahkan panjang ketiga sisinya, termasuk sisi alas. Semakin panjang sisi alas, semakin besar keliling segitiga siku-siku.
-
Rumus Keliling
Rumus keliling segitiga siku-siku melibatkan panjang sisi alas. Rumus keliling segitiga siku-siku adalah: K = s + s + m, di mana K adalah keliling, s adalah panjang sisi siku-siku, dan m adalah panjang sisi alas.
-
Aplikasi Praktis
Memahami hubungan antara sisi alas dan keliling segitiga siku-siku memiliki aplikasi praktis dalam berbagai bidang, seperti arsitektur dan teknik. Misalnya, dalam arsitektur, mengetahui keliling segitiga siku-siku penting untuk menghitung kebutuhan material dan biaya pembangunan struktur berbentuk segitiga siku-siku, seperti atap dan dinding.
Kesimpulannya, sisi alas memainkan peran penting dalam menentukan keliling segitiga siku-siku. Panjang sisi alas berdampak langsung pada nilai keliling, dan rumus keliling segitiga siku-siku memperhitungkan panjang sisi alas. Memahami hubungan ini sangat penting untuk berbagai aplikasi praktis, seperti dalam arsitektur dan teknik.
Sudut Siku-siku
Dalam segitiga siku-siku, sudut siku-siku merupakan komponen penting yang memengaruhi keliling segitiga tersebut. Sudut siku-siku adalah sudut yang besarnya 90 derajat, terbentuk oleh pertemuan dua sisi yang saling tegak lurus.
Hubungan antara sudut siku-siku dan keliling segitiga siku-siku sangat erat. Keliling segitiga siku-siku dihitung dengan menjumlahkan panjang ketiga sisinya, termasuk dua sisi yang membentuk sudut siku-siku. Dengan demikian, besar sudut siku-siku tidak secara langsung memengaruhi nilai keliling segitiga siku-siku.
Namun, sudut siku-siku memiliki peran penting dalam memastikan bahwa segitiga tersebut adalah segitiga siku-siku. Jika salah satu sudut segitiga diubah sehingga tidak lagi siku-siku, maka segitiga tersebut tidak lagi dikategorikan sebagai segitiga siku-siku dan rumus keliling segitiga siku-siku tidak lagi berlaku.
Memahami hubungan antara sudut siku-siku dan keliling segitiga siku-siku sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam arsitektur, mengetahui cara menghitung keliling segitiga siku-siku penting untuk menentukan kebutuhan material dan biaya pembangunan struktur berbentuk segitiga siku-siku, seperti atap dan dinding.
Kesimpulannya, meskipun sudut siku-siku tidak secara langsung memengaruhi nilai keliling segitiga siku-siku, namun sudut siku-siku merupakan komponen penting yang memastikan bahwa segitiga tersebut adalah segitiga siku-siku dan rumus keliling segitiga siku-siku dapat diterapkan.
FAQ Seputar Keliling Segitiga Siku-siku
Berikut ini adalah beberapa pertanyaan umum yang sering diajukan mengenai keliling segitiga siku-siku beserta jawabannya.
Pertanyaan 1: Apa yang dimaksud dengan keliling segitiga siku-siku?
Jawaban: Keliling segitiga siku-siku adalah jumlah panjang ketiga sisinya.
Pertanyaan 2: Berapa rumus untuk mencari keliling segitiga siku-siku?
Jawaban: Rumus keliling segitiga siku-siku adalah K = s + s + m, di mana K adalah keliling, s adalah panjang sisi siku-siku, dan m adalah panjang sisi miring.
Pertanyaan 3: Apakah keliling segitiga siku-siku selalu lebih besar dari panjang sisi terpanjangnya?
Jawaban: Ya, keliling segitiga siku-siku selalu lebih besar dari panjang sisi terpanjangnya.
Pertanyaan 4: Apa saja aplikasi praktis dari keliling segitiga siku-siku?
Jawaban: Keliling segitiga siku-siku memiliki banyak aplikasi praktis, seperti dalam arsitektur, teknik sipil, dan desain.
Pertanyaan 5: Siapa yang pertama kali menemukan rumus keliling segitiga siku-siku?
Jawaban: Rumus keliling segitiga siku-siku pertama kali ditemukan oleh matematikawan Yunani, Pythagoras.
Pertanyaan 6: Apakah keliling segitiga siku-siku berubah jika salah satu sudutnya diubah?
Jawaban: Tidak, keliling segitiga siku-siku tidak berubah jika salah satu sudutnya diubah, selama sisi-sisinya tetap sama.
Kesimpulan: Keliling segitiga siku-siku merupakan konsep penting dalam geometri dengan berbagai aplikasi praktis. Memahami konsep ini sangat penting untuk menyelesaikan masalah matematika, merancang struktur, dan membuat keputusan yang tepat dalam berbagai bidang.
Bagian Artikel Selanjutnya: Hubungan Keliling Segitiga Siku-siku dengan Sifat-sifatnya
Tips Seputar Keliling Segitiga Siku-Siku
Memahami keliling segitiga siku-siku sangat penting dalam berbagai bidang, seperti matematika, arsitektur, dan teknik. Berikut adalah beberapa tips untuk membantu Anda memahami dan menerapkan konsep ini secara efektif.
Youtube Video:
