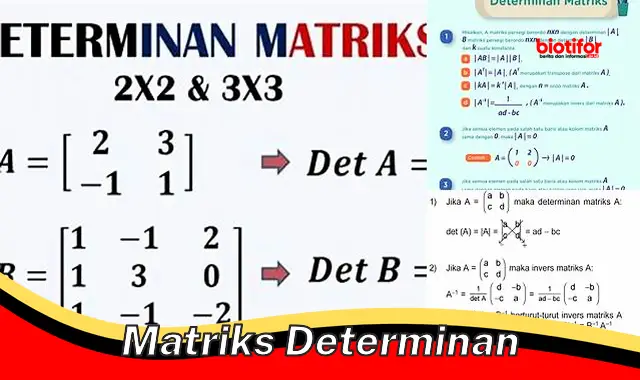
Dalam aljabar linear, matriks determinan adalah suatu besaran yang dihitung dari matriks persegi yang menunjukkan apakah matriks tersebut memiliki invers atau tidak. Determinan dari matriks persegi A berordo nxn dilambangkan dengan det(A) atau |A|.
Determinan memiliki peran penting dalam berbagai bidang matematika dan memiliki banyak aplikasi dalam sains dan teknik. Misalnya, determinan digunakan untuk mencari solusi sistem persamaan linear, mencari eigenvalues dan eigenvektor matriks, serta menghitung volume dan luas daerah yang dibatasi oleh kurva.
Secara umum, determinan matriks A berordo nxn dapat dihitung dengan menggunakan rumus Laplace atau rumus Sarrus. Rumus Laplace menyatakan determinan sebagai jumlah aljabar dari kofaktor elemen-elemen matriks, sedangkan rumus Sarrus hanya berlaku untuk matriks berordo 3×3.
Matriks Determinan
Matriks determinan memiliki beberapa aspek penting yang perlu dipahami, di antaranya:
- Ukuran matriks (ordo)
- Nilai eigen matriks
- Invers matriks
- Sistem persamaan linear
- Volume dan luas daerah
- Transformasi geometri
- Stabilitas sistem
- Teori graf
- Analisis numerik
Determinan dapat digunakan untuk menentukan apakah suatu matriks memiliki invers atau tidak. Jika determinan matriks sama dengan nol, maka matriks tersebut tidak memiliki invers. Determinan juga dapat digunakan untuk mencari nilai eigen dan eigenvektor suatu matriks, yang merupakan konsep penting dalam aljabar linear. Selain itu, determinan juga banyak digunakan dalam aplikasi lain, seperti mencari solusi sistem persamaan linear, menghitung volume dan luas daerah yang dibatasi oleh kurva, serta menganalisis stabilitas sistem.
Ukuran Matriks (Ordo)
Ukuran matriks, atau yang dikenal sebagai ordo, adalah jumlah baris dan kolom dalam matriks. Ordo matriks ditulis dalam bentuk m x n, dimana m adalah jumlah baris dan n adalah jumlah kolom. Ordo matriks memiliki pengaruh yang signifikan terhadap determinan matriks.
-
Matriks Persegi
Matriks persegi adalah matriks yang memiliki jumlah baris sama dengan jumlah kolom. Determinan matriks persegi dapat dihitung menggunakan rumus Laplace atau rumus Sarrus.
-
Matriks Non-Persegi
Matriks non-persegi adalah matriks yang memiliki jumlah baris tidak sama dengan jumlah kolom. Determinan matriks non-persegi selalu sama dengan nol.
-
Matriks Orde Tinggi
Matriks orde tinggi adalah matriks yang memiliki jumlah baris dan kolom lebih dari tiga. Determinan matriks orde tinggi dapat dihitung menggunakan metode eliminasi Gauss-Jordan atau metode kofaktor.
-
Dimensi Matriks
Dimensi matriks mengacu pada jumlah indeks yang diperlukan untuk menentukan elemen dalam matriks. Dimensi matriks selalu sama dengan ordo matriks.
Dengan demikian, ukuran matriks (ordo) merupakan aspek fundamental dalam menentukan determinan matriks. Ordo matriks menentukan metode yang digunakan untuk menghitung determinan dan juga mempengaruhi nilai determinan itu sendiri.
Nilai Eigen Matriks
Nilai eigen matriks adalah akar persamaan karakteristik matriks. Persamaan karakteristik suatu matriks A adalah det(A – I) = 0, dimana det adalah determinan, adalah nilai eigen, dan I adalah matriks identitas. Nilai eigen matriks memiliki hubungan yang erat dengan determinan matriks, yang dapat dilihat dari beberapa aspek berikut:
-
Sifat Determinan
Nilai eigen matriks merupakan akar dari polinomial karakteristik matriks, yang merupakan determinan dari matriks A – I. Oleh karena itu, determinan matriks sama dengan hasil kali nilai eigen matriks.
-
Sifat Eigenvektor
Eigenvektor yang sesuai dengan nilai eigen nol adalah vektor yang termasuk dalam kernel matriks, yang juga merupakan ruang nol determinan matriks.
-
Sifat Matriks Diagonalisasi
Matriks yang dapat didiagonalisasi memiliki himpunan eigenvektor yang menjadi basis ruang vektor tempat matriks bekerja. Determinan matriks diagonalisasi sama dengan hasil kali nilai eigen matriks.
-
Aplikasi dalam Fisika
Nilai eigen dan determinan matriks banyak digunakan dalam fisika, seperti dalam mekanika kuantum dan teori relativitas, untuk menyelesaikan masalah nilai eigen dan menentukan sifat serta perilaku sistem fisika.
Dengan demikian, nilai eigen matriks dan determinan matriks memiliki hubungan yang erat. Nilai eigen dapat diperoleh dari determinan matriks, dan determinan matriks dapat dihitung dari nilai eigen matriks. Hubungan ini sangat penting dalam aljabar linear dan memiliki aplikasi yang luas dalam matematika, fisika, dan bidang lainnya.
Invers Matriks
Invers matriks, sering dilambangkan sebagai A-1, adalah matriks yang ketika dikalikan dengan matriks asli A menghasilkan matriks identitas I. Invers matriks memiliki keterkaitan yang erat dengan matriks determinan, yang menentukan apakah suatu matriks memiliki invers atau tidak.
-
Sifat Invers Matriks
Invers matriks hanya dapat dihitung jika determinan matriks asli tidak sama dengan nol. Dengan kata lain, matriks yang memiliki determinan nol tidak memiliki invers.
-
Hubungan dengan Determinan
Determinan matriks A dan inversnya A-1 saling berkaitan, yaitu det(A-1) = 1/det(A).
-
Aplikasi dalam Persamaan Linear
Invers matriks sangat berguna dalam menyelesaikan sistem persamaan linear. Jika matriks koefisien memiliki invers, maka solusi dari sistem persamaan dapat dicari dengan mengalikan invers matriks koefisien dengan matriks konstanta.
-
Aplikasi dalam Transformasi Geometri
Invers matriks juga digunakan dalam transformasi geometri, seperti translasi, rotasi, dan penskalaan. Invers matriks transformasi mewakili transformasi kebalikan yang mengembalikan objek ke posisi semula.
Invers matriks dan matriks determinan saling terkait dalam aljabar linear. Determinan matriks menentukan apakah suatu matriks memiliki invers atau tidak, dan invers matriks dapat dicari jika determinan matriks tidak sama dengan nol. Hubungan ini menjadi dasar dalam berbagai aplikasi, termasuk penyelesaian sistem persamaan linear dan transformasi geometri.
Sistem Persamaan Linear
Sistem persamaan linear adalah sekumpulan persamaan yang melibatkan beberapa variabel yang dihubungkan dengan tanda sama dengan. Sistem persamaan linear dapat dinyatakan dalam bentuk matriks, yang kemudian dapat digunakan untuk menyelesaikan sistem persamaan tersebut.
-
Determinan dan Solusi
Determinan matriks koefisien sistem persamaan linear memainkan peran penting dalam menentukan apakah sistem tersebut memiliki solusi unik, tak hingga, atau tidak memiliki solusi. Jika determinan tidak sama dengan nol, maka sistem memiliki solusi unik. Jika determinan sama dengan nol, maka sistem dapat memiliki tak hingga solusi atau tidak memiliki solusi.
-
Kaidah Cramer
Kaidah Cramer adalah metode untuk menyelesaikan sistem persamaan linear menggunakan determinan. Kaidah ini menyatakan bahwa solusi untuk variabel xi dapat diperoleh dengan membagi determinan matriks koefisien yang kolom ke-i diganti dengan matriks konstanta dengan determinan matriks koefisien.
-
Aplikasi dalam Berbagai Bidang
Sistem persamaan linear dan determinan matriks banyak digunakan dalam berbagai bidang, seperti fisika, ekonomi, dan teknik. Misalnya, dalam fisika, sistem persamaan linear digunakan untuk menyelesaikan masalah kesetimbangan gaya, sedangkan dalam ekonomi, sistem persamaan linear digunakan untuk memodelkan sistem ekonomi.
-
Hubungan dengan Determinan
Determinan matriks koefisien sistem persamaan linear sangat penting dalam analisis sistem tersebut. Determinan memberikan informasi tentang sifat solusi sistem, seperti keberadaan solusi unik atau tak hingga. Hal ini membuat determinan menjadi alat yang sangat berguna dalam aljabar linear dan aplikasinya.
Kesimpulannya, sistem persamaan linear dan matriks determinan memiliki hubungan yang erat. Determinan matriks koefisien memberikan informasi penting tentang solusi sistem persamaan linear, seperti keberadaan solusi unik atau tak hingga. Hubungan ini sangat penting dalam aljabar linear dan memiliki aplikasi yang luas dalam berbagai bidang.
Volume dan Luas Daerah
Dalam geometri, volume dan luas daerah merupakan besaran yang penting untuk mengukur ukuran dan bentuk suatu objek. Determinan matriks memiliki hubungan yang erat dengan volume dan luas daerah, yang menjadikannya alat yang sangat berguna dalam berbagai aplikasi.
Salah satu aplikasi penting dari determinan matriks adalah dalam menghitung volume suatu parallelepiped. Parallelepiped adalah bangun ruang yang memiliki enam sisi berbentuk jajaran genjang. Volume parallelepiped dapat dihitung dengan menggunakan determinan matriks yang dibentuk oleh vektor-vektor yang mewakili sisi-sisi parallelepiped tersebut. Determinan matriks ini memberikan nilai yang sama dengan volume parallelepiped.
Selain itu, determinan matriks juga dapat digunakan untuk menghitung luas daerah suatu segitiga atau segiempat. Luas daerah suatu segitiga dapat dihitung dengan menggunakan determinan matriks yang dibentuk oleh vektor-vektor yang mewakili dua sisi segitiga tersebut. Sedangkan luas daerah suatu segiempat dapat dihitung dengan menggunakan determinan matriks yang dibentuk oleh vektor-vektor yang mewakili diagonal segiempat tersebut.
Konsep hubungan antara determinan matriks dan volume serta luas daerah sangat penting dalam berbagai bidang, seperti fisika, teknik, dan komputer grafis. Dalam fisika, misalnya, determinan matriks digunakan untuk menghitung volume dan luas permukaan benda-benda tiga dimensi. Dalam teknik, determinan matriks digunakan untuk menghitung momen inersia dan tegangan pada struktur benda. Sedangkan dalam komputer grafis, determinan matriks digunakan untuk melakukan transformasi geometri dan memproyeksikan objek tiga dimensi ke bidang dua dimensi.
Transformasi Geometri
Transformasi geometri adalah proses pemetaan suatu objek dari satu titik ke titik lainnya dalam ruang. Transformasi geometri memiliki peranan penting dalam matriks determinan, karena determinan matriks transformasi dapat menentukan sifat dan perilaku transformasi tersebut.
Determinan matriks transformasi dapat digunakan untuk menentukan apakah suatu transformasi mempertahankan luas atau volume objek. Jika determinan bernilai positif, maka transformasi mempertahankan luas atau volume. Jika determinan bernilai negatif, maka transformasi membalikkan luas atau volume. Sementara itu, jika determinan bernilai nol, maka transformasi mereduksi objek menjadi sebuah titik atau garis.
Pemahaman tentang hubungan antara transformasi geometri dan matriks determinan sangat penting dalam berbagai aplikasi, seperti:
- Grafik komputer: Determinan matriks transformasi digunakan untuk melakukan transformasi objek tiga dimensi, seperti translasi, rotasi, dan penskalaan.
- Fisika: Determinan matriks transformasi digunakan untuk menghitung momen inersia dan tegangan pada benda.
- Teknik: Determinan matriks transformasi digunakan untuk menganalisis dan mendesain struktur benda, seperti jembatan dan gedung.
Dengan demikian, hubungan antara transformasi geometri dan matriks determinan sangat penting dalam berbagai bidang, karena memungkinkan kita untuk memahami dan memanipulasi objek dalam ruang dengan cara yang efisien dan akurat.
Stabilitas Sistem
Stabilitas sistem mengacu pada kemampuan suatu sistem untuk mempertahankan kesetimbangannya saat menghadapi gangguan eksternal. Dalam konteks matriks determinan, stabilitas sistem sangat dipengaruhi oleh nilai determinan matriks tersebut.
Jika determinan matriks bernilai positif, maka sistem dikatakan stabil. Ini berarti bahwa setiap gangguan kecil pada sistem akan menyebabkan sistem kembali ke keadaan kesetimbangannya. Sebaliknya, jika determinan bernilai negatif, maka sistem dikatakan tidak stabil. Gangguan kecil pada sistem akan menyebabkan sistem menyimpang dari keadaan kesetimbangannya dan berpotensi menjadi tidak terkendali.
Dalam praktiknya, stabilitas sistem sangat penting dalam berbagai bidang, seperti:
- Teknik: Stabilitas sistem penting dalam desain sistem kontrol, seperti pada pesawat terbang dan roket, untuk memastikan bahwa sistem tetap stabil dan dapat dikendalikan dalam berbagai kondisi operasi.
- Ekonomi: Stabilitas sistem penting dalam pemodelan sistem ekonomi, seperti pasar keuangan, untuk memprediksi dan mencegah fluktuasi yang tidak diinginkan.
- Biologi: Stabilitas sistem penting dalam memahami dinamika populasi dan ekosistem, untuk memprediksi dan mencegah perubahan mendadak yang dapat membahayakan kelangsungan hidup spesies.
Dengan memahami hubungan antara stabilitas sistem dan matriks determinan, kita dapat mengembangkan sistem yang lebih stabil dan andal di berbagai bidang.
Teori Graf
Teori graf adalah cabang matematika yang mempelajari struktur dan sifat-sifat graf. Graf adalah representasi abstrak dari suatu sistem kompleks yang terdiri dari sekumpulan simpul yang dihubungkan oleh sisi. Dalam konteks matriks determinan, teori graf memiliki peran penting dalam menganalisis sifat-sifat graf dan memecahkan masalah terkait graf.
-
Representasi Matriks
Setiap graf dapat direpresentasikan dalam bentuk matriks yang disebut matriks adjasensi. Matriks adjasensi adalah matriks persegi yang elemen-elemennya menunjukkan apakah terdapat sisi antara dua simpul tertentu dalam graf. Matriks determinan dari matriks adjasensi dapat memberikan informasi penting tentang sifat-sifat graf, seperti apakah graf terhubung atau tidak.
-
Orientasi Graf
Teori graf juga dapat digunakan untuk menganalisis graf berorientasi, yaitu graf yang sisinya memiliki arah. Matriks determinan dari matriks insidensi graf berorientasi dapat memberikan informasi tentang sifat-sifat orientasi graf, seperti apakah graf tersebut kuat atau tidak.
-
Pohon Rentang
Pohon rentang adalah subgraf dari suatu graf yang menghubungkan semua simpul tanpa membentuk siklus. Teori graf dapat digunakan untuk mencari pohon rentang dengan menggunakan algoritma seperti algoritma Kruskal atau algoritma Prim. Determinan matriks Laplacian dari suatu graf dapat digunakan untuk menghitung berat total pohon rentang minimum.
-
Teorema Tutte
Teorema Tutte adalah teorema penting dalam teori graf yang menghubungkan determinan matriks Kirchhoff suatu graf dengan jumlah pasangan potongan bebas dalam graf tersebut. Teorema ini memiliki aplikasi dalam berbagai bidang, seperti kimia dan fisika.
Dengan demikian, teori graf dan matriks determinan memiliki hubungan yang erat. Teori graf menyediakan cara untuk merepresentasikan dan menganalisis struktur graf, sementara matriks determinan dapat memberikan informasi penting tentang sifat-sifat graf dan memecahkan masalah terkait graf.
Analisis Numerik
Analisis numerik adalah cabang matematika yang berfokus pada pengembangan metode dan algoritma untuk menyelesaikan masalah matematika secara numerik. Dalam konteks matriks determinan, analisis numerik memainkan peran penting dalam menghitung determinan matriks secara efisien dan akurat.
Salah satu metode yang umum digunakan dalam analisis numerik untuk menghitung determinan matriks adalah metode eliminasi Gauss-Jordan. Metode ini melibatkan serangkaian operasi baris elementer, seperti penjumlahan, pengurangan, dan perkalian, untuk mengubah matriks menjadi matriks eselon baris tereduksi. Determinan matriks kemudian dapat diperoleh dengan mengalikan elemen-elemen diagonal dari matriks yang telah tereduksi.
Selain metode eliminasi Gauss-Jordan, ada metode lain yang dapat digunakan untuk menghitung determinan matriks, seperti metode kofaktor dan metode Laplace. Namun, metode eliminasi Gauss-Jordan umumnya lebih efisien untuk matriks berukuran besar.
Pemahaman tentang hubungan antara analisis numerik dan matriks determinan sangat penting dalam berbagai aplikasi praktis, seperti:
- Persamaan Diferensial Numerik: Menentukan determinan matriks koefisien diperlukan untuk menyelesaikan persamaan diferensial numerik dengan metode numerik, seperti metode beda hingga atau metode elemen hingga.
- Regresi Linier: Analisis numerik digunakan untuk menghitung determinan matriks kovariansi dalam regresi linier, yang sangat penting untuk menentukan kecocokan model regresi dan memperkirakan parameter model.
- Optimasi Numerik: Determinan matriks Hessian digunakan dalam optimasi numerik untuk menentukan titik ekstrem dari suatu fungsi. Pengetahuan tentang determinan matriks Hessian memungkinkan kita untuk mengidentifikasi titik maksimum atau minimum lokal dari fungsi tersebut.
Dengan demikian, analisis numerik dan matriks determinan memiliki hubungan yang erat. Analisis numerik menyediakan metode untuk menghitung determinan matriks secara efisien, yang sangat penting dalam berbagai aplikasi praktis di bidang matematika, fisika, teknik, dan ilmu komputer.
Pertanyaan Umum tentang Matriks Determinan
Berikut adalah beberapa pertanyaan umum tentang matriks determinan beserta jawabannya:
Pertanyaan 1: Apa itu matriks determinan?
Jawaban: Matriks determinan adalah besaran yang dihitung dari matriks persegi yang menunjukkan apakah matriks tersebut memiliki invers atau tidak.
Pertanyaan 2: Mengapa matriks determinan penting?
Jawaban: Matriks determinan memiliki peran penting dalam berbagai bidang matematika dan memiliki banyak aplikasi dalam sains dan teknik, seperti mencari solusi sistem persamaan linear, mencari eigenvalues dan eigenvektor matriks, serta menghitung volume dan luas daerah.
Pertanyaan 3: Bagaimana cara menghitung matriks determinan?
Jawaban: Determinan matriks A berordo nxn dapat dihitung dengan menggunakan rumus Laplace atau rumus Sarrus.
Pertanyaan 4: Apa hubungan antara matriks determinan dan invers matriks?
Jawaban: Matriks determinan menentukan apakah suatu matriks memiliki invers atau tidak. Jika determinan matriks sama dengan nol, maka matriks tersebut tidak memiliki invers.
Pertanyaan 5: Apa aplikasi matriks determinan dalam kehidupan nyata?
Jawaban: Matriks determinan memiliki banyak aplikasi dalam kehidupan nyata, seperti dalam teknik, fisika, ekonomi, dan komputer grafis.
Pertanyaan 6: Apa saja sifat-sifat matriks determinan?
Jawaban: Matriks determinan memiliki beberapa sifat penting, seperti sifat aditif, sifat perkalian, dan sifat determinan invers.
Selain pertanyaan yang disebutkan di atas, masih banyak pertanyaan lain yang dapat diajukan tentang matriks determinan. Dengan memahami konsep-konsep dasar matriks determinan, kita dapat menjawab pertanyaan-pertanyaan tersebut dan mengaplikasikannya dalam berbagai bidang.
Untuk mempelajari lebih lanjut tentang matriks determinan, Anda dapat merujuk ke buku-buku atau sumber daya online yang tersedia.
Tips Menguasai Matriks Determinan
Menguasai matriks determinan membutuhkan pemahaman konsep yang mendalam dan latihan yang teratur. Berikut adalah beberapa tips yang dapat membantu Anda menguasai topik ini:
Tip 1: Pahami Konsep Dasar
Sebelum mempelajari matriks determinan, penting untuk memiliki dasar yang kuat dalam aljabar linear, termasuk operasi matriks dan sifat-sifat determinan.
Tip 2: Latih Menghitung Determinan
Keterampilan menghitung determinan sangat penting. Berlatihlah menghitung determinan matriks berordo 2×2, 3×3, dan seterusnya menggunakan rumus Laplace atau rumus Sarrus.
Tip 3: Kuasai Sifat-Sifat Determinan
Memahami sifat-sifat determinan, seperti sifat aditif, perkalian, dan invers, akan membantu Anda menyelesaikan masalah determinan dengan lebih mudah.
Tip 4: Manfaatkan Teknologi
Meskipun menghitung determinan dapat dilakukan secara manual, Anda dapat menggunakan kalkulator atau perangkat lunak matematika untuk menghitung determinan matriks berukuran besar.
Tip 5: Terapkan dalam Masalah Nyata
Terapkan konsep matriks determinan dalam masalah nyata, seperti mencari solusi sistem persamaan linear, mencari eigenvalues dan eigenvektor, atau menghitung volume dan luas daerah.
Tip 6: Belajar dari Kesalahan
Jangan takut membuat kesalahan saat mempelajari matriks determinan. Kesalahan justru menjadi kesempatan untuk belajar dan memahami konsep dengan lebih baik.
Tip 7: Konsisten Belajar dan Berlatih
Menguasai matriks determinan membutuhkan konsistensi dalam belajar dan berlatih. Luangkan waktu secara teratur untuk mempelajari materi dan mengerjakan soal-soal latihan.
Tip 8: Cari Bantuan jika Diperlukan
Jika Anda kesulitan memahami konsep matriks determinan, jangan ragu untuk mencari bantuan dari guru, tutor, atau teman yang lebih paham.
Dengan mengikuti tips ini dan berdedikasi untuk belajar, Anda dapat menguasai matriks determinan dan menerapkannya dalam berbagai aplikasi di berbagai bidang.
Kesimpulan
Matriks determinan merupakan konsep penting dalam aljabar linear dengan beragam aplikasi di berbagai bidang. Determinan memberikan informasi tentang sifat-sifat matriks, seperti keterbalikan dan stabilitas sistem. Pemahaman mendalam tentang matriks determinan sangat penting untuk menyelesaikan masalah matematika kompleks dan menerapkannya dalam dunia nyata.
Menguasai matriks determinan membutuhkan pemahaman konsep yang kuat dan latihan yang teratur. Dengan mengikuti tips yang telah dibahas sebelumnya, Anda dapat menguasai topik ini dan memanfaatkannya untuk memecahkan masalah dan mengembangkan solusi inovatif di berbagai bidang.
Youtube Video:
