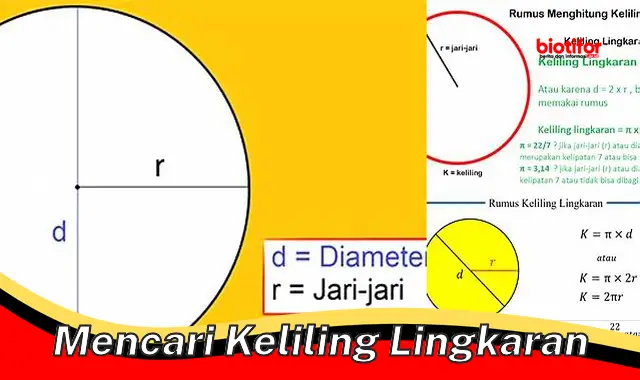
Mencari keliling lingkaran adalah proses menentukan jarak di sekitar tepi lingkaran. Rumus untuk mencari keliling lingkaran adalah 2r, di mana adalah konstanta matematika sekitar 3,14 dan r adalah jari-jari lingkaran.
Mencari keliling lingkaran sangat penting dalam berbagai bidang, termasuk teknik, arsitektur, dan desain. Misalnya, dalam teknik, keliling lingkaran digunakan untuk menghitung panjang kabel atau pipa yang diperlukan untuk melilit objek melingkar. Dalam arsitektur, keliling lingkaran digunakan untuk menentukan jumlah bahan yang dibutuhkan untuk membangun struktur berbentuk lingkaran, seperti kubah atau rotunda. Dalam desain, keliling lingkaran digunakan untuk menentukan ukuran kanvas atau bingkai yang diperlukan untuk memajang karya seni berbentuk lingkaran.
Secara historis, pencarian keliling lingkaran telah menjadi masalah penting dalam matematika. Pada abad ke-3 SM, Archimedes mengembangkan metode untuk memperkirakan keliling lingkaran menggunakan poligon beraturan. Metode ini kemudian disempurnakan oleh matematikawan lain sepanjang sejarah, dan pada abad ke-17, Isaac Newton mengembangkan rumus untuk keliling lingkaran yang masih digunakan hingga sekarang.
mencari keliling lingkaran
Mencari keliling lingkaran merupakan aspek penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Berikut adalah 10 aspek penting yang terkait dengan mencari keliling lingkaran:
- Rumus: 2r
- Konstanta
- Jari-jari (r)
- Diameter
- Keliling
- Aplikasi dalam teknik
- Aplikasi dalam arsitektur
- Aplikasi dalam desain
- Sejarah pencarian keliling lingkaran
- Metode Archimedes
Aspek-aspek ini saling terkait dan membentuk dasar untuk memahami cara mencari keliling lingkaran. Misalnya, rumus untuk mencari keliling lingkaran (2r) tidak dapat digunakan tanpa memahami konsep jari-jari (r) dan konstanta . Selain itu, aplikasi mencari keliling lingkaran dalam teknik, arsitektur, dan desain menunjukkan pentingnya aspek ini dalam kehidupan nyata.
Rumus
Rumus keliling lingkaran, 2r, merupakan rumus penting yang digunakan untuk mencari panjang tepi lingkaran. Rumus ini menyatakan bahwa keliling lingkaran sama dengan 2r, di mana adalah konstanta matematika sekitar 3,14 dan r adalah jari-jari lingkaran.
-
Konstanta
Konstanta adalah bilangan irasional yang tidak dapat dinyatakan sebagai pecahan sederhana. Nilai sekitar 3,14 dan merupakan rasio keliling lingkaran terhadap diameternya. -
Jari-jari (r)
Jari-jari lingkaran adalah jarak dari pusat lingkaran ke tepi lingkaran. Dalam rumus 2r, jari-jari dilambangkan dengan huruf r. -
Aplikasi dalam berbagai bidang
Rumus keliling lingkaran digunakan dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Misalnya, dalam teknik, rumus ini digunakan untuk menghitung panjang kabel atau pipa yang diperlukan untuk melilit objek melingkar. -
Sejarah
Rumus keliling lingkaran telah dikenal sejak zaman dahulu. Pada abad ke-3 SM, Archimedes mengembangkan metode untuk memperkirakan keliling lingkaran menggunakan poligon beraturan. Metode ini kemudian disempurnakan oleh matematikawan lain sepanjang sejarah, dan pada abad ke-17, Isaac Newton mengembangkan rumus 2r yang masih digunakan hingga sekarang.
Rumus 2r merupakan alat yang ampuh untuk mencari keliling lingkaran. Rumus ini mudah digunakan dan memberikan hasil yang akurat. Rumus ini juga memiliki dasar matematika yang kuat dan telah digunakan selama berabad-abad.
Konstanta
Konstanta merupakan bilangan irasional yang tidak dapat dinyatakan sebagai pecahan sederhana. Nilai sekitar 3,14 dan merupakan rasio keliling lingkaran terhadap diameternya. Konstanta memiliki peran penting dalam matematika, fisika, dan teknik, termasuk dalam mencari keliling lingkaran.
Dalam mencari keliling lingkaran, konstanta digunakan sebagai faktor pengali jari-jari lingkaran. Rumus keliling lingkaran adalah 2r, di mana r adalah jari-jari lingkaran. Konstanta memastikan bahwa rumus ini memberikan hasil yang akurat, yaitu panjang tepi lingkaran.
Contoh penerapan konstanta dalam mencari keliling lingkaran dapat ditemukan dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Misalnya, dalam teknik, konstanta digunakan untuk menghitung panjang kabel atau pipa yang diperlukan untuk melilit objek melingkar. Dalam arsitektur, konstanta digunakan untuk menentukan jumlah bahan yang dibutuhkan untuk membangun struktur berbentuk lingkaran, seperti kubah atau rotunda. Dalam desain, konstanta digunakan untuk menentukan ukuran kanvas atau bingkai yang diperlukan untuk memajang karya seni berbentuk lingkaran.
Memahami hubungan antara konstanta dan mencari keliling lingkaran sangat penting untuk memastikan akurasi dan keandalan hasil perhitungan. Dengan memahami peran penting dalam rumus keliling lingkaran, kita dapat memperoleh hasil yang tepat dan membuat keputusan yang tepat berdasarkan hasil tersebut.
Jari-jari (r)
Jari-jari (r) memegang peranan penting dalam mencari keliling lingkaran. Jari-jari merupakan jarak dari pusat lingkaran ke tepi lingkaran, dan berperan sebagai faktor pengali dalam rumus keliling lingkaran, yaitu 2r.
-
Ukuran Lingkaran
Jari-jari menentukan ukuran lingkaran. Semakin besar jari-jari, semakin besar keliling lingkaran. -
Aplikasi dalam Teknik
Dalam teknik, jari-jari digunakan untuk menghitung panjang kabel atau pipa yang diperlukan untuk melilit objek melingkar. Misalnya, untuk menentukan panjang kabel yang dibutuhkan untuk melilitkan kumparan motor. -
Aplikasi dalam Arsitektur
Dalam arsitektur, jari-jari digunakan untuk menentukan ukuran struktur berbentuk lingkaran, seperti kubah atau rotunda. Misalnya, untuk menghitung jumlah bahan yang dibutuhkan untuk membangun kubah dengan jari-jari tertentu. -
Aplikasi dalam Desain
Dalam desain, jari-jari digunakan untuk menentukan ukuran kanvas atau bingkai untuk memajang karya seni berbentuk lingkaran. Misalnya, untuk menentukan ukuran bingkai yang sesuai untuk lukisan berbentuk lingkaran.
Dengan memahami hubungan antara jari-jari dan keliling lingkaran, kita dapat menghitung keliling lingkaran secara akurat dan membuat keputusan berdasarkan informasi dalam berbagai bidang, seperti teknik, arsitektur, dan desain.
Diameter
Diameter memiliki hubungan erat dengan mencari keliling lingkaran. Diameter adalah garis lurus yang melalui pusat lingkaran dan menghubungkan dua titik pada tepi lingkaran. Diameter lingkaran sama dengan dua kali jari-jarinya, atau d = 2r.
Dalam mencari keliling lingkaran, diameter dapat digunakan sebagai alternatif jari-jari dalam rumus keliling lingkaran. Rumus keliling lingkaran menggunakan diameter adalah: K = d di mana:
- K adalah keliling lingkaran
- d adalah diameter lingkaran
Rumus ini dapat digunakan untuk mencari keliling lingkaran ketika diameternya diketahui.
Contoh penerapan hubungan antara diameter dan mencari keliling lingkaran dapat ditemukan dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Misalnya, dalam teknik, diameter digunakan untuk menentukan ukuran pipa atau kabel yang dibutuhkan untuk aplikasi tertentu. Dalam arsitektur, diameter digunakan untuk menentukan ukuran kubah atau rotunda. Dalam desain, diameter digunakan untuk menentukan ukuran kanvas atau bingkai untuk memajang karya seni berbentuk lingkaran.
Dengan memahami hubungan antara diameter dan mencari keliling lingkaran, kita dapat menghitung keliling lingkaran secara akurat dan membuat keputusan berdasarkan informasi dalam berbagai bidang.
Keliling
Keliling adalah panjang tepi suatu bangun datar tertutup, termasuk lingkaran. Mencari keliling lingkaran merupakan aspek penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain.
Dalam mencari keliling lingkaran, keliling berperan sebagai besaran yang akan dihitung. Keliling lingkaran memiliki rumus khusus, yaitu 2r atau d, di mana adalah konstanta matematika sekitar 3,14, r adalah jari-jari lingkaran, dan d adalah diameter lingkaran. Rumus-rumus ini digunakan untuk menghitung panjang tepi lingkaran berdasarkan jari-jari atau diameternya.
Memahami hubungan antara keliling dan mencari keliling lingkaran sangat penting dalam kehidupan nyata. Misalnya, dalam teknik, keliling lingkaran digunakan untuk menghitung panjang kabel atau pipa yang diperlukan untuk melilit suatu objek. Dalam arsitektur, keliling lingkaran digunakan untuk menentukan ukuran bahan yang dibutuhkan untuk membangun struktur berbentuk lingkaran, seperti kubah atau rotunda. Dalam desain, keliling lingkaran digunakan untuk menentukan ukuran kanvas atau bingkai yang diperlukan untuk memajang karya seni berbentuk lingkaran.
Dengan memahami konsep keliling dan cara mencari keliling lingkaran, kita dapat membuat keputusan yang tepat dan menyelesaikan masalah yang melibatkan lingkaran dalam berbagai bidang.
Aplikasi dalam teknik
Dalam bidang teknik, mencari keliling lingkaran memiliki peran penting dalam berbagai aspek, terutama yang melibatkan objek atau struktur berbentuk lingkaran. Berikut adalah beberapa aspek yang menghubungkan aplikasi dalam teknik dengan pencarian keliling lingkaran:
-
Perhitungan Panjang Kabel atau Pipa
Dalam sistem kelistrikan atau perpipaan, teknisi perlu menentukan panjang kabel atau pipa yang dibutuhkan untuk melilit atau membungkus objek berbentuk lingkaran, seperti motor listrik atau tangki penyimpanan. Dengan menggunakan rumus keliling lingkaran, mereka dapat menghitung panjang yang tepat untuk memastikan fungsi yang optimal. -
Desain Gear dan Katrol
Keliling lingkaran juga berperan penting dalam desain gear dan katrol. Teknisi perlu menghitung keliling lingkaran roda gigi atau katrol untuk memastikan kesesuaian dan rasio yang tepat dalam sistem transmisi daya. -
Konstruksi Bangunan Berbentuk Lingkaran
Dalam konstruksi, mencari keliling lingkaran digunakan untuk menentukan jumlah bahan yang dibutuhkan untuk membangun struktur berbentuk lingkaran, seperti kubah atau tangki air. Dengan menghitung keliling lingkaran, kontraktor dapat memperkirakan kebutuhan material secara akurat untuk memastikan stabilitas dan integritas struktural. -
Perancangan Jalan dan Rel Kereta
Dalam teknik sipil, keliling lingkaran digunakan dalam perancangan jalan dan rel kereta yang melengkung. Dengan menghitung keliling lingkaran, insinyur dapat menentukan radius dan sudut lengkung yang sesuai untuk memastikan keselamatan dan kelancaran lalu lintas.
Dengan memahami hubungan antara mencari keliling lingkaran dan aplikasinya dalam teknik, kita dapat mengapresiasi pentingnya aspek ini dalam memecahkan masalah teknis, merancang sistem yang efisien, dan memastikan integritas struktural dalam berbagai proyek teknik.
Aplikasi dalam arsitektur
Hubungan antara aplikasi dalam arsitektur dan mencari keliling lingkaran sangat erat, karena keliling lingkaran menjadi dasar penting dalam merancang dan membangun berbagai struktur arsitektur.
-
Desain Struktur Melengkung
Dalam mendesain struktur melengkung seperti kubah, rotunda, dan lengkungan, arsitek menggunakan keliling lingkaran untuk menentukan ukuran dan bentuk struktur. Keliling lingkaran menentukan panjang lengkungan dan membantu memastikan stabilitas serta estetika struktur. -
Perhitungan Bahan Bangunan
Saat merencanakan konstruksi struktur berbentuk lingkaran, arsitek perlu menghitung jumlah bahan bangunan yang dibutuhkan, seperti batu bata, beton, atau kaca. Mencari keliling lingkaran memungkinkan arsitek memperkirakan jumlah bahan yang dibutuhkan secara akurat, meminimalkan pemborosan dan memastikan efisiensi biaya. -
Desain Interior dan Eksterior
Dalam desain interior dan eksterior, arsitek menggunakan keliling lingkaran untuk menciptakan elemen dekoratif seperti jendela berbentuk lingkaran, kolom melingkar, dan tangga spiral. Keliling lingkaran membantu memastikan proporsi dan keseimbangan yang tepat dalam desain, menghasilkan ruang interior dan eksterior yang estetis dan fungsional. -
Perencanaan Lansekap
Dalam perencanaan lansekap, arsitek lansekap menggunakan keliling lingkaran untuk mendesain elemen seperti jalur taman melingkar, kolam berbentuk lingkaran, dan fitur air mancur. Keliling lingkaran memungkinkan mereka menciptakan ruang luar yang harmonis dan estetis, memberikan keseimbangan dan keteraturan pada lanskap.
Dengan memahami hubungan antara aplikasi dalam arsitektur dan mencari keliling lingkaran, kita dapat mengapresiasi peran penting aspek ini dalam menciptakan struktur dan ruang yang indah, fungsional, dan tahan lama.
Aplikasi dalam desain
Hubungan antara aplikasi dalam desain dan mencari keliling lingkaran sangat erat, karena keliling lingkaran merupakan faktor penting dalam menciptakan desain yang estetis dan fungsional.
Dalam desain grafis, keliling lingkaran digunakan untuk membuat logo, ikon, dan elemen desain lainnya. Desainer menggunakan rumus keliling lingkaran untuk memastikan proporsi dan keseimbangan yang tepat dalam desain mereka. Keliling lingkaran juga digunakan untuk membuat grafik dan diagram melingkar, yang merupakan alat visual yang efektif untuk menyajikan data dan informasi.
Dalam desain produk, keliling lingkaran digunakan untuk menentukan dimensi dan bentuk produk. Misalnya, keliling lingkaran digunakan untuk menentukan ukuran piring, mangkuk, dan benda berbentuk lingkaran lainnya. Keliling lingkaran juga digunakan dalam desain furnitur, seperti meja, kursi, dan lampu, untuk menciptakan bentuk dan ukuran yang ergonomis dan estetis.
Dalam desain web, keliling lingkaran digunakan untuk membuat elemen desain seperti tombol, menu, dan ikon navigasi. Desainer menggunakan rumus keliling lingkaran untuk memastikan bahwa elemen-elemen ini memiliki ukuran dan bentuk yang konsisten, menciptakan pengalaman pengguna yang intuitif dan menyenangkan.
Memahami hubungan antara aplikasi dalam desain dan mencari keliling lingkaran sangat penting bagi desainer untuk menciptakan desain yang efektif dan menarik. Dengan menggunakan rumus keliling lingkaran, desainer dapat memastikan bahwa desain mereka memiliki proporsi yang tepat, bentuk yang estetis, dan fungsionalitas yang optimal.
Sejarah pencarian keliling lingkaran
Sejarah pencarian keliling lingkaran merupakan bagian integral dari perkembangan matematika dan geometri. Sejak zaman kuno, para matematikawan telah berupaya mencari metode yang akurat untuk menentukan keliling lingkaran.
-
Metode Archimedes
Salah satu metode paling awal untuk mencari keliling lingkaran dikembangkan oleh Archimedes pada abad ke-3 SM. Metode ini melibatkan penggunaan poligon beraturan yang di inscribed dan circumscribed pada lingkaran. Archimedes membuktikan bahwa semakin banyak sisi poligon, semakin dekat keliling poligon dengan keliling lingkaran. Metode ini memberikan perkiraan keliling lingkaran yang akurat, dan menjadi dasar bagi pengembangan metode selanjutnya.
-
Metode Leibniz
Pada abad ke-17, Gottfried Leibniz mengembangkan metode baru untuk mencari keliling lingkaran menggunakan deret tak hingga. Metode ini melibatkan pembagian keliling lingkaran menjadi bagian-bagian kecil yang tak hingga, dan kemudian menjumlahkan panjang bagian-bagian tersebut untuk mendapatkan keliling lingkaran. Metode Leibniz memberikan pendekatan yang lebih akurat dibandingkan metode Archimedes, dan menjadi dasar bagi pengembangan metode modern untuk mencari keliling lingkaran.
-
Metode Monte Carlo
Pada abad ke-20, metode Monte Carlo dikembangkan sebagai pendekatan numerik untuk mencari keliling lingkaran. Metode ini melibatkan pengambilan sampel titik acak di dalam lingkaran dan menggunakan sampel tersebut untuk memperkirakan keliling lingkaran. Metode Monte Carlo memberikan perkiraan yang cukup akurat, dan sering digunakan dalam aplikasi komputasi.
-
Rumus Modern
Rumus modern untuk mencari keliling lingkaran, yaitu 2r, dikembangkan berdasarkan metode-metode sebelumnya. Rumus ini menggunakan konstanta (pi), yang merupakan rasio keliling lingkaran terhadap diameternya. Rumus ini memberikan hasil yang sangat akurat dan menjadi metode standar untuk mencari keliling lingkaran dalam aplikasi praktis.
Sejarah pencarian keliling lingkaran menunjukkan bahwa pencarian solusi yang akurat untuk masalah ini telah menjadi pendorong utama perkembangan matematika. Metode-metode yang dikembangkan dari zaman kuno hingga modern telah memberikan pemahaman yang lebih baik tentang keliling lingkaran dan membantu kita memecahkan masalah praktis yang melibatkan bentuk melingkar.
Metode Archimedes
Metode Archimedes merupakan salah satu metode awal untuk mencari keliling lingkaran yang dikembangkan oleh matematikawan Yunani, Archimedes, pada abad ke-3 SM. Metode ini menjadi komponen penting dalam mencari keliling lingkaran karena memberikan pendekatan yang akurat dan menjadi dasar bagi pengembangan metode selanjutnya.
Metode Archimedes didasarkan pada konsep membagi keliling lingkaran menjadi bagian-bagian yang lebih kecil, yaitu dengan cara meng-inscribe dan meng-circumscribe poligon beraturan pada lingkaran. Archimedes membuktikan bahwa semakin banyak sisi poligon, maka keliling poligon akan semakin mendekati keliling lingkaran. Dengan menggunakan prinsip ini, ia dapat memperkirakan keliling lingkaran dengan tingkat akurasi yang tinggi.
Praktisnya, metode Archimedes telah digunakan dalam berbagai bidang yang membutuhkan perhitungan keliling lingkaran, seperti teknik, arsitektur, dan desain. Misalnya, dalam teknik, metode ini digunakan untuk menghitung panjang kabel atau pipa yang diperlukan untuk melilitkan suatu objek berbentuk lingkaran. Dalam arsitektur, metode ini digunakan untuk menentukan ukuran kolom atau lengkungan berbentuk lingkaran dalam suatu bangunan.
Memahami hubungan antara Metode Archimedes dan mencari keliling lingkaran sangatlah penting karena memberikan dasar teoretis untuk menghitung keliling lingkaran secara akurat. Metode ini menjadi kontribusi penting dalam perkembangan matematika dan geometri, serta terus digunakan hingga saat ini untuk menyelesaikan masalah praktis yang melibatkan bentuk lingkaran.
Pertanyaan Umum tentang Mencari Keliling Lingkaran
Pertanyaan 1: Apa itu keliling lingkaran?
Keliling lingkaran adalah panjang tepinya. Keliling lingkaran dihitung menggunakan rumus 2r, di mana r adalah jari-jari lingkaran.
Pertanyaan 2: Bagaimana cara mencari keliling lingkaran?
Untuk mencari keliling lingkaran, gunakan rumus 2r. Misalnya, jika jari-jari lingkaran adalah 5 cm, maka keliling lingkarannya adalah 2 x 5 cm = 10 cm.
Pertanyaan 3: Apa saja aplikasi mencari keliling lingkaran?
Mencari keliling lingkaran memiliki banyak aplikasi dalam kehidupan nyata, seperti dalam teknik, arsitektur, dan desain. Misalnya, dalam teknik, keliling lingkaran digunakan untuk menghitung panjang kabel yang dibutuhkan untuk melilitkan motor listrik.
Pertanyaan 4: Siapa yang pertama kali menemukan rumus keliling lingkaran?
Rumus keliling lingkaran pertama kali ditemukan oleh matematikawan Yunani, Archimedes, pada abad ke-3 SM.
Pertanyaan 5: Apa saja metode yang digunakan untuk mencari keliling lingkaran?
Selain menggunakan rumus, terdapat beberapa metode lain yang dapat digunakan untuk mencari keliling lingkaran, seperti metode Archimedes, metode Leibniz, dan metode Monte Carlo.
Pertanyaan 6: Mengapa penting untuk memahami cara mencari keliling lingkaran?
Memahami cara mencari keliling lingkaran sangat penting karena dapat membantu kita memecahkan masalah praktis yang melibatkan bentuk lingkaran. Misalnya, dalam arsitektur, keliling lingkaran digunakan untuk menghitung jumlah bahan yang dibutuhkan untuk membangun kubah berbentuk lingkaran.
Dengan memahami konsep dan aplikasi mencari keliling lingkaran, kita dapat memperoleh hasil yang akurat dan membuat keputusan berdasarkan informasi dalam berbagai bidang.
Kesimpulan:
Mencari keliling lingkaran adalah aspek penting dalam berbagai bidang, dan terdapat metode yang berbeda untuk menghitungnya secara akurat. Pemahaman yang baik tentang cara mencari keliling lingkaran dapat membantu kita menyelesaikan masalah praktis dan membuat keputusan yang tepat.
Tips Mencari Keliling Lingkaran
Mencari keliling lingkaran merupakan aspek penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Berikut beberapa tips untuk membantu Anda mencari keliling lingkaran secara akurat dan efisien:
Tip 1: Gunakan Rumus yang Tepat
Gunakan rumus keliling lingkaran yang sesuai, yaitu 2r, di mana r adalah jari-jari lingkaran. Pastikan Anda menggunakan satuan yang sama untuk jari-jari dan keliling, seperti sentimeter atau meter.
Tip 2: Identifikasi Jari-jari
Jari-jari lingkaran adalah jarak dari pusat lingkaran ke tepinya. Jika jari-jari tidak diketahui, Anda dapat mengukurnya menggunakan penggaris atau jangka sorong.
Tip 3: Manfaatkan Kalkulator
Jika perhitungan keliling lingkaran melibatkan angka desimal, gunakan kalkulator untuk mendapatkan hasil yang akurat. Masukkan nilai jari-jari ke dalam rumus dan hitung kelilingnya.
Tip 4: Gunakan Metode Alternatif
Selain rumus, terdapat metode lain untuk mencari keliling lingkaran, seperti metode Archimedes atau metode Monte Carlo. Metode ini dapat digunakan untuk memperkirakan keliling lingkaran ketika jari-jari tidak diketahui atau sulit diukur.
Tip 5: Verifikasi Hasil
Setelah menghitung keliling lingkaran, verifikasi hasilnya dengan mengukur keliling lingkaran secara langsung menggunakan pita pengukur atau alat ukur lainnya. Hal ini akan membantu memastikan akurasi perhitungan Anda.
Dengan mengikuti tips ini, Anda dapat mencari keliling lingkaran secara akurat dan efisien. Kemahiran dalam mencari keliling lingkaran sangat bermanfaat dalam berbagai bidang dan dapat membantu Anda memecahkan masalah praktis dengan efektif.
Kesimpulan
Mencari keliling lingkaran merupakan aspek krusial dalam berbagai bidang, mulai dari teknik hingga desain. Pemahaman yang baik tentang konsep dan aplikasinya sangat penting untuk menyelesaikan masalah praktis dan membuat keputusan yang tepat.
Artikel ini telah mengeksplorasi secara komprehensif berbagai aspek terkait pencarian keliling lingkaran, termasuk rumus, metode alternatif, aplikasi di berbagai bidang, sejarah perkembangan, dan tips untuk mencari keliling lingkaran secara akurat. Dengan menguasai konsep-konsep ini, individu dapat memperoleh keterampilan penting dan berkontribusi secara efektif dalam bidang yang membutuhkan pemahaman tentang keliling lingkaran.
Youtube Video:
