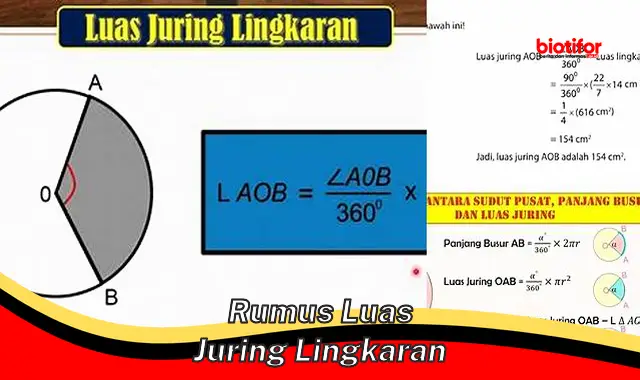
Rumus luas juring lingkaran adalah rumus yang digunakan untuk menghitung luas daerah yang dibatasi oleh dua jari-jari dan sebuah busur lingkaran. Rumus ini dinyatakan dengan:
L = (1/2) x r^2 x
di mana:
– L adalah luas juring lingkaran (dalam satuan luas)
– r adalah jari-jari lingkaran (dalam satuan panjang)
– adalah sudut pusat yang membentuk juring lingkaran (dalam satuan radian)
Rumus luas juring lingkaran sangat penting dalam berbagai bidang, seperti:
– Arsitektur: Untuk menghitung luas jendela atau pintu yang berbentuk juring lingkaran
– Teknik: Untuk menghitung luas roda gigi atau katrol yang berbentuk juring lingkaran
– Matematika: Untuk menyelesaikan masalah geometri yang melibatkan juring lingkaran
Selain itu, rumus luas juring lingkaran juga memiliki sejarah yang panjang. Rumus ini pertama kali ditemukan oleh Archimedes pada abad ke-3 SM. Archimedes menggunakan rumus ini untuk menghitung luas segmen parabola. Seiring berjalannya waktu, rumus ini dikembangkan dan disempurnakan oleh para ahli matematika lainnya, hingga akhirnya menjadi rumus yang kita gunakan sekarang.
Rumus Luas Juring Lingkaran
Rumus luas juring lingkaran sangat penting dalam berbagai bidang, karena dapat digunakan untuk menyelesaikan masalah yang melibatkan bentuk juring lingkaran. Beberapa aspek penting yang terkait dengan rumus luas juring lingkaran antara lain:
- Pengertian: Rumus yang digunakan untuk menghitung luas daerah yang dibatasi oleh dua jari-jari dan sebuah busur lingkaran.
- Penemu: Archimedes, pada abad ke-3 SM.
- Bentuk: L = (1/2) x r^2 x , di mana L adalah luas juring lingkaran, r adalah jari-jari lingkaran, dan adalah sudut pusat yang membentuk juring lingkaran.
- Satuan: Luas (m^2, cm^2, dll).
- Aplikasi: Arsitektur, teknik, matematika.
- Manfaat: Memudahkan perhitungan luas juring lingkaran.
- Sejarah: Telah dikembangkan dan disempurnakan oleh para ahli matematika selama berabad-abad.
- Contoh: Menghitung luas jendela berbentuk juring lingkaran, menghitung luas roda gigi berbentuk juring lingkaran, menghitung luas segmen parabola.
Dengan memahami berbagai aspek penting yang terkait dengan rumus luas juring lingkaran, kita dapat lebih mudah menggunakan dan menerapkan rumus ini dalam berbagai bidang yang membutuhkan.
Pengertian
Pengertian ini merupakan definisi dari “rumus luas juring lingkaran”. Rumus luas juring lingkaran adalah rumus yang digunakan untuk menghitung luas daerah yang dibatasi oleh dua jari-jari dan sebuah busur lingkaran. Pengertian ini penting karena memberikan dasar pemahaman tentang apa itu rumus luas juring lingkaran dan bagaimana rumus tersebut digunakan.
Tanpa pengertian yang jelas tentang definisi rumus luas juring lingkaran, akan sulit untuk memahami dan menerapkan rumus tersebut dengan benar. Oleh karena itu, pengertian ini merupakan komponen penting dari rumus luas juring lingkaran dan sangat penting untuk dipahami sebelum menggunakan rumus tersebut.
Sebagai contoh, dalam bidang arsitektur, rumus luas juring lingkaran digunakan untuk menghitung luas jendela atau pintu yang berbentuk juring lingkaran. Tanpa memahami pengertian dari rumus luas juring lingkaran, seorang arsitek akan kesulitan untuk menghitung luas jendela atau pintu tersebut dengan benar.
Dengan memahami pengertian dari rumus luas juring lingkaran, kita dapat lebih mudah menggunakan dan menerapkan rumus tersebut dalam berbagai bidang yang membutuhkan, seperti arsitektur, teknik, dan matematika.
Penemu
Archimedes, seorang matematikawan dan fisikawan Yunani, menemukan rumus luas juring lingkaran pada abad ke-3 SM. Penemuan ini sangat penting dalam perkembangan matematika, khususnya geometri. Rumus tersebut memungkinkan para ahli matematika dan ilmuwan untuk menghitung luas daerah yang dibatasi oleh dua jari-jari dan sebuah busur lingkaran.
-
Peran Archimedes
Archimedes memainkan peran penting dalam penemuan rumus luas juring lingkaran. Ia mengembangkan metode yang dikenal sebagai “metode penghabisan” untuk menghitung luas daerah lengkung, termasuk juring lingkaran. Metode ini melibatkan pembagian juring lingkaran menjadi segitiga-segitiga kecil dan kemudian menghitung luas masing-masing segitiga. Dengan menjumlahkan luas semua segitiga, Archimedes dapat memperoleh perkiraan luas juring lingkaran.
-
Contoh Aplikasi
Rumus luas juring lingkaran telah digunakan dalam berbagai aplikasi selama berabad-abad. Beberapa contoh aplikasi tersebut antara lain:
– Arsitektur: Menghitung luas jendela atau pintu yang berbentuk juring lingkaran.
– Teknik: Menghitung luas roda gigi atau katrol yang berbentuk juring lingkaran.
– Matematika: Menyelesaikan masalah geometri yang melibatkan juring lingkaran. -
Implikasi dalam Rumus Luas Juring Lingkaran
Penemuan Archimedes tentang rumus luas juring lingkaran memiliki implikasi yang luas dalam pengembangan rumus tersebut. Rumus tersebut menjadi dasar bagi pengembangan rumus-rumus lain yang terkait dengan lingkaran, seperti rumus keliling lingkaran dan rumus luas lingkaran. Selain itu, rumus luas juring lingkaran juga telah digunakan sebagai dasar untuk mengembangkan rumus-rumus yang lebih kompleks, seperti rumus luas elips dan rumus luas hiperbola.
Dengan demikian, penemuan Archimedes tentang rumus luas juring lingkaran merupakan kontribusi penting dalam bidang matematika. Rumus tersebut telah digunakan secara luas dalam berbagai aplikasi dan menjadi dasar bagi pengembangan rumus-rumus lain yang lebih kompleks.
Bentuk
Bentuk rumus luas juring lingkaran, yaitu L = (1/2) x r^2 x , memiliki hubungan yang erat dengan konsep rumus luas juring lingkaran itu sendiri. Bentuk rumus ini merupakan representasi matematis dari konsep luas juring lingkaran, yang didefinisikan sebagai luas daerah yang dibatasi oleh dua jari-jari dan sebuah busur lingkaran.
Dalam bentuk rumus tersebut, variabel L mewakili luas juring lingkaran, r mewakili jari-jari lingkaran, dan mewakili sudut pusat yang membentuk juring lingkaran. Ketiga variabel ini merupakan komponen penting dalam menentukan luas juring lingkaran. Luas juring lingkaran akan berbanding lurus dengan kuadrat jari-jari lingkaran dan sudut pusat yang membentuk juring lingkaran.
Sebagai contoh, jika jari-jari lingkaran diperbesar dua kali, maka luas juring lingkaran akan menjadi empat kali lebih besar. Demikian pula, jika sudut pusat yang membentuk juring lingkaran diperbesar dua kali, maka luas juring lingkaran akan menjadi dua kali lebih besar. Hubungan ini tercermin dalam bentuk rumus luas juring lingkaran, yaitu L = (1/2) x r^2 x .
Memahami bentuk rumus luas juring lingkaran sangat penting karena memungkinkan kita untuk menghitung luas juring lingkaran dengan mudah dan akurat. Rumus ini banyak digunakan dalam berbagai bidang, seperti arsitektur, teknik, dan matematika. Dengan memahami bentuk rumus ini, kita dapat menyelesaikan masalah yang melibatkan juring lingkaran dengan lebih efektif.
Satuan
Satuan luas merupakan komponen penting dalam rumus luas juring lingkaran karena digunakan untuk menyatakan hasil perhitungan luas juring lingkaran. Luas juring lingkaran diukur dalam satuan luas, seperti meter persegi (m^2), sentimeter persegi (cm^2), dan sebagainya.
Pemilihan satuan luas yang tepat sangat penting untuk memastikan bahwa hasil perhitungan luas juring lingkaran sesuai dengan konteks penggunaannya. Misalnya, jika kita menghitung luas jendela berbentuk juring lingkaran, maka satuan luas yang tepat adalah meter persegi (m^2). Sebaliknya, jika kita menghitung luas roda gigi berbentuk juring lingkaran, maka satuan luas yang tepat adalah sentimeter persegi (cm^2).
Oleh karena itu, memahami hubungan antara satuan luas dan rumus luas juring lingkaran sangat penting untuk memastikan bahwa hasil perhitungan luas juring lingkaran akurat dan sesuai dengan kebutuhan. Kesalahan dalam pemilihan satuan luas dapat menyebabkan kesalahan dalam perhitungan luas juring lingkaran, yang pada akhirnya dapat berdampak pada keputusan atau tindakan yang diambil berdasarkan perhitungan tersebut.
Aplikasi
Rumus luas juring lingkaran memiliki peran penting dalam berbagai bidang aplikasi, terutama dalam arsitektur, teknik, dan matematika. Berikut adalah beberapa aspek penting yang menyoroti hubungan antara rumus luas juring lingkaran dengan bidang-bidang tersebut:
-
Arsitektur
Dalam arsitektur, rumus luas juring lingkaran digunakan untuk menghitung luas jendela atau pintu yang berbentuk juring lingkaran. Misalnya, seorang arsitek dapat menggunakan rumus ini untuk menghitung luas jendela berbentuk setengah lingkaran pada sebuah gedung. Dengan mengetahui luas juring lingkaran, arsitek dapat merencanakan ukuran dan tata letak jendela secara optimal.
-
Teknik
Dalam teknik, rumus luas juring lingkaran digunakan untuk menghitung luas roda gigi atau katrol yang berbentuk juring lingkaran. Misalnya, seorang insinyur dapat menggunakan rumus ini untuk menghitung luas roda gigi pada sebuah mesin. Dengan mengetahui luas juring lingkaran, insinyur dapat menentukan ukuran dan bentuk roda gigi yang sesuai.
-
Matematika
Dalam matematika, rumus luas juring lingkaran digunakan untuk menyelesaikan masalah geometri yang melibatkan juring lingkaran. Misalnya, seorang siswa dapat menggunakan rumus ini untuk menghitung luas segmen parabola. Dengan memahami rumus luas juring lingkaran, siswa dapat memecahkan masalah geometri yang kompleks.
Hubungan antara rumus luas juring lingkaran dengan bidang aplikasi tersebut menunjukkan bahwa rumus ini merupakan alat yang penting dan serbaguna dalam berbagai bidang. Dengan memahami dan menerapkan rumus ini, para profesional dan siswa dapat menyelesaikan masalah dan merancang solusi secara efektif di bidang arsitektur, teknik, dan matematika.
Manfaat
Rumus luas juring lingkaran sangat bermanfaat karena memudahkan perhitungan luas daerah yang dibatasi oleh dua jari-jari dan sebuah busur lingkaran. Rumus ini sangat penting dalam berbagai bidang, seperti arsitektur, teknik, dan matematika. Tanpa rumus ini, menghitung luas juring lingkaran akan menjadi proses yang sulit dan memakan waktu.
-
Menghemat waktu dan tenaga
Dengan menggunakan rumus luas juring lingkaran, kita dapat menghitung luas juring lingkaran dengan cepat dan mudah. Hal ini menghemat banyak waktu dan tenaga dibandingkan dengan metode penghitungan lainnya, seperti menggunakan integral atau membagi juring lingkaran menjadi segitiga-segitiga kecil.
-
Meningkatkan akurasi
Rumus luas juring lingkaran memberikan hasil yang akurat. Hal ini penting dalam berbagai aplikasi, seperti desain arsitektur dan teknik, di mana akurasi perhitungan sangat penting.
-
Memfasilitasi pemecahan masalah
Rumus luas juring lingkaran dapat digunakan untuk menyelesaikan berbagai masalah matematika dan teknik yang melibatkan juring lingkaran. Misalnya, rumus ini dapat digunakan untuk menghitung luas segmen parabola atau menentukan sudut pusat suatu juring lingkaran.
Dengan demikian, kemudahan penghitungan yang disediakan oleh rumus luas juring lingkaran menjadikannya alat yang sangat bermanfaat dalam berbagai bidang. Rumus ini menghemat waktu dan tenaga, meningkatkan akurasi, dan memfasilitasi pemecahan masalah.
Sejarah
Rumus luas juring lingkaran memiliki sejarah panjang yang mencerminkan perkembangan pemikiran matematika selama berabad-abad. Perjalanan pengembangan rumus ini melibatkan kontribusi dari para ahli matematika terkemuka, sehingga menjadikannya sebuah rumus yang akurat dan dapat diandalkan untuk menghitung luas juring lingkaran.
-
Perkembangan Awal
Konsep awal luas juring lingkaran dapat ditelusuri kembali ke zaman dahulu, di mana para matematikawan seperti Archimedes menggunakan metode penghabisan untuk memperkirakan luas daerah lengkung. Metode ini melibatkan pembagian juring lingkaran menjadi segitiga-segitiga kecil dan menghitung luas masing-masing segitiga.
-
Kontribusi Matematikawan Muslim
Matematikawan Muslim, seperti Al-Biruni dan Omar Khayyam, memberikan kontribusi signifikan terhadap pengembangan rumus luas juring lingkaran. Mereka memperkenalkan teknik-teknik baru untuk menghitung luas juring lingkaran, termasuk penggunaan trigonometri dan kalkulus.
-
Perkembangan di Eropa
Selama Renaissance di Eropa, matematikawan seperti Johannes Kepler dan Ren Descartes melanjutkan pengembangan rumus luas juring lingkaran. Mereka menyempurnakan metode yang ada dan memperluas penerapan rumus tersebut ke bidang-bidang baru.
-
Rumus Modern
Bentuk modern dari rumus luas juring lingkaran, yang kita gunakan saat ini, dikembangkan pada abad ke-17 oleh Sir Isaac Newton dan Gottfried Wilhelm Leibniz. Rumus ini didasarkan pada konsep kalkulus dan memberikan hasil yang sangat akurat.
Perjalanan pengembangan rumus luas juring lingkaran selama berabad-abad ini menunjukkan pentingnya kolaborasi dan kemajuan bertahap dalam matematika. Rumus yang kita gunakan saat ini adalah hasil dari kontribusi banyak ahli matematika selama berabad-abad, sehingga menjadikannya alat yang sangat berharga untuk menghitung luas juring lingkaran dalam berbagai aplikasi.
Contoh
Rumus luas juring lingkaran sangat penting karena memiliki banyak aplikasi dalam kehidupan nyata, seperti menghitung luas jendela berbentuk juring lingkaran, menghitung luas roda gigi berbentuk juring lingkaran, dan menghitung luas segmen parabola.
Contoh-contoh tersebut menunjukkan pentingnya rumus luas juring lingkaran sebagai komponen penting dalam berbagai bidang. Dalam arsitektur, rumus ini digunakan untuk menentukan luas jendela berbentuk juring lingkaran. Jendela seperti ini sering digunakan pada bangunan-bangunan dengan desain melengkung atau pada atap kubah. Menghitung luas jendela secara akurat sangat penting untuk memastikan pencahayaan dan ventilasi yang optimal di dalam ruangan.
Dalam teknik mesin, rumus luas juring lingkaran juga sangat penting. Roda gigi berbentuk juring lingkaran banyak digunakan dalam berbagai mesin dan perangkat. Menghitung luas roda gigi secara akurat sangat penting untuk memastikan bahwa roda gigi tersebut dapat bekerja dengan baik dan efisien.
Selain itu, rumus luas juring lingkaran juga digunakan dalam matematika untuk menghitung luas segmen parabola. Segmen parabola sering muncul dalam berbagai aplikasi, seperti fisika dan teknik sipil. Menghitung luas segmen parabola secara akurat sangat penting untuk menyelesaikan masalah-masalah yang melibatkan bentuk lengkung.
Kesimpulannya, contoh-contoh yang disebutkan di atas menunjukkan bahwa rumus luas juring lingkaran memiliki peran yang sangat penting dalam berbagai bidang. Rumus ini memungkinkan kita untuk menghitung luas daerah yang dibatasi oleh dua jari-jari dan sebuah busur lingkaran dengan mudah dan akurat. Pemahaman tentang rumus luas juring lingkaran dan aplikasi-aplikasinya sangat penting bagi para profesional dan siswa di berbagai bidang, seperti arsitektur, teknik, dan matematika.
Pertanyaan yang Sering Diajukan Seputar Rumus Luas Juring Lingkaran
Berikut adalah beberapa pertanyaan yang sering diajukan terkait rumus luas juring lingkaran:
Pertanyaan 1: Apa itu rumus luas juring lingkaran?
Jawaban: Rumus luas juring lingkaran adalah rumus yang digunakan untuk menghitung luas daerah yang dibatasi oleh dua jari-jari dan sebuah busur lingkaran. Rumus tersebut dinyatakan sebagai berikut: L = (1/2) x r^2 x , di mana L adalah luas juring lingkaran, r adalah jari-jari lingkaran, dan adalah sudut pusat yang membentuk juring lingkaran.
Pertanyaan 2: Mengapa rumus luas juring lingkaran penting?
Jawaban: Rumus luas juring lingkaran sangat penting karena memiliki banyak aplikasi dalam berbagai bidang, seperti arsitektur, teknik, dan matematika. Rumus ini memungkinkan kita untuk menghitung luas daerah yang dibatasi oleh dua jari-jari dan sebuah busur lingkaran dengan mudah dan akurat.
Pertanyaan 3: Bagaimana cara menggunakan rumus luas juring lingkaran?
Jawaban: Untuk menggunakan rumus luas juring lingkaran, Anda perlu mengetahui nilai jari-jari lingkaran (r) dan sudut pusat yang membentuk juring lingkaran (). Setelah itu, Anda dapat mensubstitusikan nilai tersebut ke dalam rumus L = (1/2) x r^2 x dan menghitung luas juring lingkaran.
Pertanyaan 4: Apa satuan dari luas juring lingkaran?
Jawaban: Satuan luas juring lingkaran adalah satuan luas, seperti meter persegi (m^2), sentimeter persegi (cm^2), dan sebagainya. Pemilihan satuan luas harus disesuaikan dengan konteks penggunaan rumus.
Pertanyaan 5: Dalam bidang apa saja rumus luas juring lingkaran digunakan?
Jawaban: Rumus luas juring lingkaran digunakan dalam berbagai bidang, seperti arsitektur untuk menghitung luas jendela atau pintu berbentuk juring lingkaran, teknik untuk menghitung luas roda gigi atau katrol berbentuk juring lingkaran, dan matematika untuk menyelesaikan masalah geometri yang melibatkan juring lingkaran.
Pertanyaan 6: Siapakah yang menemukan rumus luas juring lingkaran?
Jawaban: Rumus luas juring lingkaran ditemukan oleh Archimedes, seorang matematikawan dan fisikawan Yunani, pada abad ke-3 SM.
Demikianlah beberapa pertanyaan yang sering diajukan tentang rumus luas juring lingkaran. Dengan memahami rumus ini dan aplikasinya, kita dapat menyelesaikan masalah dan merancang solusi secara efektif di berbagai bidang.
Kembali ke atas
Tips Menggunakan Rumus Luas Juring Lingkaran
Rumus luas juring lingkaran sangat penting dalam berbagai bidang, seperti arsitektur, teknik, dan matematika. Untuk menggunakan rumus ini secara efektif, berikut beberapa tips yang dapat diikuti:
Tip 1: Pahami Konsep Juring Lingkaran
Sebelum menggunakan rumus, pastikan Anda memahami konsep juring lingkaran. Juring lingkaran adalah daerah yang dibatasi oleh dua jari-jari dan sebuah busur lingkaran.
Tip 2: Identifikasi Jari-jari dan Sudut Pusat
Untuk menggunakan rumus, Anda perlu mengetahui nilai jari-jari lingkaran (r) dan sudut pusat yang membentuk juring lingkaran ().
Tip 3: Gunakan Satuan yang Tepat
Hasil perhitungan luas juring lingkaran harus dinyatakan dalam satuan luas yang sesuai, seperti meter persegi (m2) atau sentimeter persegi (cm2).
Tip 4: Perhatikan Akurasi Pengukuran
Akurasi hasil perhitungan sangat bergantung pada akurasi pengukuran jari-jari dan sudut pusat juring lingkaran.
Tip 5: Gunakan Kalkulator atau Alat Bantu Lainnya
Untuk memudahkan perhitungan, gunakan kalkulator atau alat bantu lainnya seperti penggaris atau busur derajat.
Tip 6: Periksa Kembali Hasil
Setelah melakukan perhitungan, periksa kembali hasil Anda untuk memastikan keakuratannya.
Dengan mengikuti tips ini, Anda dapat menggunakan rumus luas juring lingkaran secara efektif untuk menyelesaikan masalah dan merancang solusi di berbagai bidang.
Kembali ke atas
Kesimpulan Rumus Luas Juring Lingkaran
Rumus luas juring lingkaran merupakan rumus yang penting dan serbaguna dalam berbagai bidang, seperti arsitektur, teknik, dan matematika. Rumus ini memungkinkan kita untuk menentukan luas daerah yang dibatasi oleh dua jari-jari dan sebuah busur lingkaran secara akurat dan efisien.
Dalam aplikasinya, rumus luas juring lingkaran sangat membantu dalam merancang dan menyelesaikan masalah yang melibatkan juring lingkaran. Pemahaman yang baik tentang rumus ini menjadi bekal yang sangat berharga bagi para profesional dan siswa di berbagai bidang.
Youtube Video:
