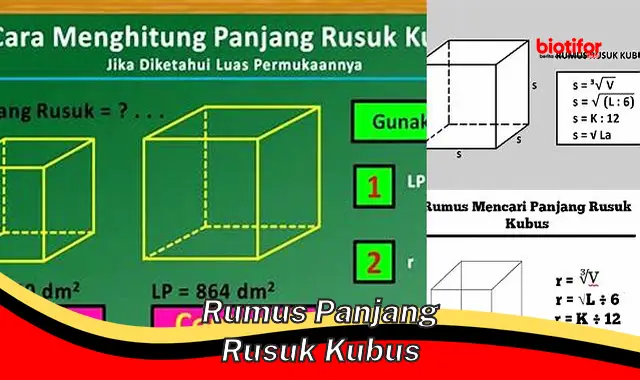
Rumus panjang rusuk kubus adalah sebuah rumus yang digunakan untuk menghitung panjang rusuk sebuah kubus. Rumus ini menyatakan bahwa panjang rusuk kubus sama dengan akar pangkat tiga dari volume kubus tersebut.
Rumus panjang rusuk kubus sangat penting dalam berbagai bidang, seperti arsitektur, teknik, dan matematika. Rumus ini digunakan untuk menghitung ukuran berbagai objek, seperti balok, kubus, dan prisma. Selain itu, rumus ini juga digunakan untuk menghitung volume berbagai benda, seperti kubus, balok, dan limas.
Secara historis, rumus panjang rusuk kubus pertama kali ditemukan oleh matematikawan Yunani kuno, Euclid. Rumus ini tercatat dalam buku Euclid yang berjudul “Elements”. Rumus ini kemudian digunakan oleh matematikawan lain selama berabad-abad, dan hingga saat ini masih digunakan secara luas.
Rumus Panjang Rusuk Kubus
Rumus panjang rusuk kubus merupakan rumus penting dalam matematika dan memiliki berbagai aspek penting yang saling berkaitan.
- Definisi
- Volume
- Dimensi
- Aplikasi
- Sejarah
- Jenis-jenis Kubus
- Luas Permukaan
- Diagonal Ruang
- Diagonal Bidang
Definisi rumus panjang rusuk kubus adalah menyatakan bahwa panjang rusuk kubus sama dengan akar pangkat tiga dari volume kubus tersebut. Rumus ini memiliki keterkaitan dengan volume kubus, dimana volume kubus dapat dihitung dengan mengalikan panjang rusuk kubus dengan dirinya sendiri sebanyak tiga kali. Selain itu, rumus ini juga berkaitan dengan dimensi kubus, dimana kubus memiliki tiga dimensi yaitu panjang, lebar, dan tinggi yang sama. Rumus panjang rusuk kubus juga memiliki aplikasi dalam berbagai bidang, seperti arsitektur, teknik, dan matematika. Dalam bidang arsitektur, rumus ini digunakan untuk menghitung ukuran balok, kubus, dan prisma. Dalam bidang teknik, rumus ini digunakan untuk menghitung volume berbagai benda, seperti kubus, balok, dan limas. Dalam bidang matematika, rumus ini digunakan untuk menghitung panjang diagonal ruang dan diagonal bidang kubus.
Definisi Rumus Panjang Rusuk Kubus
Definisi rumus panjang rusuk kubus adalah pernyataan yang menyatakan bahwa panjang rusuk kubus sama dengan akar pangkat tiga dari volume kubus tersebut. Definisi ini memiliki beberapa aspek penting, antara lain:
- Rumus: s = V, di mana s adalah panjang rusuk kubus dan V adalah volume kubus.
- Volume: Volume kubus dihitung dengan mengalikan panjang rusuk kubus dengan dirinya sendiri sebanyak tiga kali, yaitu V = s.
- Panjang Rusuk: Panjang rusuk kubus adalah panjang sisi kubus yang sama pada semua sisinya.
Definisi rumus panjang rusuk kubus sangat penting dalam matematika dan memiliki berbagai aplikasi dalam berbagai bidang. Definisi ini menjadi dasar untuk memahami dan menggunakan rumus panjang rusuk kubus dalam berbagai perhitungan dan pemecahan masalah.
Volume
Volume adalah besaran yang menyatakan banyaknya ruang yang ditempati oleh suatu benda. Dalam konteks rumus panjang rusuk kubus, volume memiliki peran yang sangat penting karena menjadi dasar untuk menghitung panjang rusuk kubus tersebut.
-
Menghitung Panjang Rusuk Kubus
Rumus panjang rusuk kubus menyatakan bahwa panjang rusuk kubus sama dengan akar pangkat tiga dari volume kubus tersebut. Hal ini berarti bahwa untuk menghitung panjang rusuk kubus, kita perlu mengetahui volume kubus terlebih dahulu.
-
Satuan Volume
Satuan volume yang umum digunakan adalah meter kubik (m), liter (L), dan mililiter (mL). Dalam konteks rumus panjang rusuk kubus, satuan volume yang digunakan harus konsisten dengan satuan panjang yang digunakan untuk menghitung panjang rusuk kubus.
-
Contoh Penerapan
Rumus panjang rusuk kubus dapat diterapkan dalam berbagai bidang, seperti arsitektur, teknik, dan matematika. Misalnya, dalam arsitektur, rumus ini digunakan untuk menghitung volume ruang suatu bangunan.
-
Rumus Terkait
Selain rumus panjang rusuk kubus, terdapat juga rumus-rumus lain yang berkaitan dengan volume kubus, seperti rumus volume kubus (V = s) dan rumus luas permukaan kubus (L = 6s).
Dengan memahami hubungan antara volume dan rumus panjang rusuk kubus, kita dapat menghitung panjang rusuk kubus dengan mudah dan akurat. Rumus ini sangat penting dalam berbagai bidang dan memiliki banyak aplikasi dalam kehidupan sehari-hari.
Dimensi
Dimensi memiliki keterkaitan yang erat dengan rumus panjang rusuk kubus karena kubus merupakan bangun ruang tiga dimensi. Dimensi sebuah kubus ditentukan oleh panjang, lebar, dan tingginya, yang semuanya sama besar.
-
Panjang, Lebar, dan Tinggi
Panjang, lebar, dan tinggi merupakan tiga dimensi sebuah kubus. Ketiga dimensi ini memiliki nilai yang sama, sehingga kubus memiliki bentuk yang simetris.
-
Volume
Volume kubus dihitung dengan mengalikan panjang, lebar, dan tinggi kubus. Karena ketiga dimensi tersebut sama, maka volume kubus dapat dihitung dengan menggunakan rumus V = s, di mana s adalah panjang rusuk kubus.
-
Luas Permukaan
Luas permukaan kubus dihitung dengan menjumlahkan luas keenam sisi kubus. Karena keenam sisi kubus berbentuk persegi dengan panjang sisi s, maka luas permukaan kubus dapat dihitung dengan rumus L = 6s.
-
Diagonal Ruang
Diagonal ruang kubus adalah ruas garis yang menghubungkan dua titik sudut kubus yang berhadapan. Diagonal ruang kubus dapat dihitung menggunakan rumus d = s3, di mana s adalah panjang rusuk kubus.
Dengan memahami keterkaitan antara dimensi dan rumus panjang rusuk kubus, kita dapat menghitung berbagai besaran yang berhubungan dengan kubus, seperti volume, luas permukaan, dan diagonal ruang kubus.
Aplikasi
Rumus panjang rusuk kubus memiliki berbagai aplikasi dalam kehidupan sehari-hari. Beberapa aplikasi penting antara lain:
- Arsitektur: Rumus panjang rusuk kubus digunakan untuk menghitung volume dan luas permukaan bangunan yang berbentuk kubus atau balok.
- Teknik: Rumus panjang rusuk kubus digunakan untuk menghitung volume benda-benda yang berbentuk kubus atau balok, seperti balok es, tangki air, dan kotak.
- Matematika: Rumus panjang rusuk kubus digunakan dalam berbagai soal matematika, seperti menghitung volume dan luas permukaan kubus, serta menghitung diagonal ruang dan diagonal bidang kubus.
- Fisika: Rumus panjang rusuk kubus digunakan untuk menghitung volume benda-benda yang berbentuk kubus atau balok, seperti volume sebuah kubus es atau volume sebuah balok kayu.
- Kimia: Rumus panjang rusuk kubus digunakan untuk menghitung volume zat kimia yang berbentuk kubus atau balok, seperti volume sebuah kubus natrium klorida atau volume sebuah balok parafin.
Penguasaan rumus panjang rusuk kubus sangat penting dalam berbagai bidang karena memungkinkan kita untuk menghitung volume dan luas permukaan benda-benda yang berbentuk kubus atau balok dengan mudah dan akurat. Rumus ini juga menjadi dasar untuk memahami dan menyelesaikan berbagai soal matematika dan fisika yang berkaitan dengan kubus dan balok.
Sejarah
Sejarah memiliki keterkaitan yang erat dengan rumus panjang rusuk kubus karena rumus tersebut ditemukan dan dikembangkan melalui proses panjang yang melibatkan banyak matematikawan dan ilmuwan selama berabad-abad.
Salah satu tokoh penting dalam sejarah rumus panjang rusuk kubus adalah matematikawan Yunani kuno, Euclid. Dalam bukunya yang berjudul “Elements”, Euclid mengemukakan teorema yang menyatakan bahwa volume kubus sama dengan panjang rusuk kubus dipangkatkan tiga. Teorema ini menjadi dasar bagi pengembangan rumus panjang rusuk kubus.
Matematikawan lain yang berkontribusi pada pengembangan rumus panjang rusuk kubus adalah Archimedes. Archimedes menemukan rumus untuk menghitung volume bola dan kerucut, yang kemudian digunakan untuk menghitung volume kubus. Selain itu, Archimedes juga mengembangkan metode untuk menghitung panjang rusuk kubus menggunakan prinsip pengungkit.
Rumus panjang rusuk kubus yang kita gunakan saat ini merupakan hasil pengembangan dari karya matematikawan dan ilmuwan selama berabad-abad. Rumus ini telah menjadi alat penting dalam berbagai bidang, seperti arsitektur, teknik, dan matematika.
Jenis-jenis Kubus
Rumus panjang rusuk kubus memiliki keterkaitan dengan jenis-jenis kubus yang ada. Kubus memiliki beberapa jenis, antara lain:
-
Kubus Siku-siku
Kubus siku-siku adalah kubus yang memiliki panjang rusuk yang sama pada ketiga dimensinya (panjang, lebar, dan tinggi). Kubus siku-siku merupakan jenis kubus yang paling umum dan banyak digunakan dalam berbagai aplikasi.
-
Kubus Miring
Kubus miring adalah kubus yang memiliki panjang rusuk yang berbeda pada ketiga dimensinya. Kubus miring dapat berbentuk segitiga siku-siku atau belah ketupat.
-
Kubus Terpotong
Kubus terpotong adalah kubus yang memiliki salah satu atau lebih sisinya terpotong. Kubus terpotong dapat berbentuk balok atau prisma.
-
Kubus Berongga
Kubus berongga adalah kubus yang memiliki rongga atau ruang kosong di dalamnya. Kubus berongga dapat berbentuk kubus dengan lubang atau kubus dengan rongga yang lebih kompleks.
Masing-masing jenis kubus memiliki rumus panjang rusuk yang berbeda. Rumus panjang rusuk kubus siku-siku adalah s = V, di mana s adalah panjang rusuk kubus dan V adalah volume kubus. Rumus panjang rusuk kubus miring, terpotong, dan berongga lebih kompleks dan melibatkan perhitungan tambahan.
Luas Permukaan
Luas permukaan merupakan besaran yang menyatakan besarnya permukaan suatu benda. Dalam konteks rumus panjang rusuk kubus, luas permukaan memiliki keterkaitan yang erat karena menjadi salah satu faktor yang menentukan panjang rusuk kubus tersebut.
Rumus panjang rusuk kubus menyatakan bahwa panjang rusuk kubus sama dengan akar pangkat tiga dari volume kubus tersebut. Volume kubus sendiri dapat dihitung dengan mengalikan luas permukaan kubus dengan panjang rusuk kubus. Dengan demikian, luas permukaan kubus menjadi faktor penting dalam menentukan panjang rusuk kubus.
Dalam kehidupan sehari-hari, pemahaman tentang hubungan antara luas permukaan dan rumus panjang rusuk kubus sangat bermanfaat. Misalnya, dalam arsitektur, luas permukaan kubus digunakan untuk menghitung luas dinding dan atap sebuah bangunan yang berbentuk kubus. Dalam teknik, luas permukaan kubus digunakan untuk menghitung luas permukaan benda-benda yang berbentuk kubus, seperti balok es atau tangki air.
Dengan memahami hubungan antara luas permukaan dan rumus panjang rusuk kubus, kita dapat menghitung panjang rusuk kubus dengan mudah dan akurat. Pemahaman ini juga menjadi dasar untuk memahami dan menyelesaikan berbagai soal matematika dan fisika yang berkaitan dengan kubus.
Diagonal Ruang
Diagonal ruang kubus adalah ruas garis yang menghubungkan dua titik sudut kubus yang berhadapan. Diagonal ruang memiliki keterkaitan yang erat dengan rumus panjang rusuk kubus karena dapat digunakan untuk menentukan panjang rusuk kubus tersebut.
-
Definisi Diagonal Ruang
Diagonal ruang kubus adalah ruas garis yang menghubungkan dua titik sudut kubus yang berhadapan. Panjang diagonal ruang dapat dihitung menggunakan rumus d = s3, di mana d adalah diagonal ruang dan s adalah panjang rusuk kubus.
-
Hubungan dengan Panjang Rusuk Kubus
Diagonal ruang kubus memiliki hubungan yang erat dengan panjang rusuk kubus. Panjang diagonal ruang dapat digunakan untuk menentukan panjang rusuk kubus menggunakan rumus s = d/3, di mana s adalah panjang rusuk kubus dan d adalah diagonal ruang.
-
Aplikasi dalam Kehidupan Nyata
Diagonal ruang kubus memiliki berbagai aplikasi dalam kehidupan nyata, seperti:
– Arsitektur: Diagonal ruang kubus digunakan untuk menentukan panjang diagonal ruang bangunan yang berbentuk kubus.
– Teknik: Diagonal ruang kubus digunakan untuk menentukan panjang diagonal ruang benda-benda yang berbentuk kubus, seperti balok es atau tangki air. -
Contoh Soal
Sebuah kubus memiliki diagonal ruang sepanjang 10 cm. Tentukan panjang rusuk kubus tersebut.
Jawab:
d = s3
10 = s3
s = 10/3
s = 5,77 cm
Dengan memahami hubungan antara diagonal ruang dan rumus panjang rusuk kubus, kita dapat menentukan panjang rusuk kubus dengan mudah dan akurat. Pemahaman ini juga menjadi dasar untuk memahami dan menyelesaikan berbagai soal matematika dan fisika yang berkaitan dengan kubus.
Diagonal Bidang
Diagonal bidang kubus adalah ruas garis yang menghubungkan dua titik sudut kubus yang tidak terletak pada sisi yang sama. Diagonal bidang memiliki keterkaitan yang erat dengan rumus panjang rusuk kubus karena dapat digunakan untuk menentukan panjang rusuk kubus tersebut.
Rumus panjang rusuk kubus menyatakan bahwa panjang rusuk kubus sama dengan akar pangkat tiga dari volume kubus tersebut. Volume kubus sendiri dapat dihitung dengan mengalikan luas permukaan kubus dengan panjang rusuk kubus. Dengan demikian, diagonal bidang kubus menjadi faktor penting dalam menentukan panjang rusuk kubus.
Dalam kehidupan sehari-hari, pemahaman tentang hubungan antara diagonal bidang dan rumus panjang rusuk kubus sangat bermanfaat. Misalnya, dalam arsitektur, diagonal bidang kubus digunakan untuk menghitung panjang diagonal bidang bangunan yang berbentuk kubus. Dalam teknik, diagonal bidang kubus digunakan untuk menghitung panjang diagonal bidang benda-benda yang berbentuk kubus, seperti balok es atau tangki air.
Dengan memahami hubungan antara diagonal bidang dan rumus panjang rusuk kubus, kita dapat menentukan panjang rusuk kubus dengan mudah dan akurat. Pemahaman ini juga menjadi dasar untuk memahami dan menyelesaikan berbagai soal matematika dan fisika yang berkaitan dengan kubus.
Pertanyaan Umum tentang Rumus Panjang Rusuk Kubus
Rumus panjang rusuk kubus merupakan rumus yang penting dalam matematika dan memiliki berbagai aspek penting yang saling berkaitan. Berikut adalah beberapa pertanyaan umum yang sering diajukan tentang rumus panjang rusuk kubus:
-
Apa itu rumus panjang rusuk kubus?
Rumus panjang rusuk kubus adalah s = V, di mana s adalah panjang rusuk kubus dan V adalah volume kubus.
-
Bagaimana cara menggunakan rumus panjang rusuk kubus?
Untuk menggunakan rumus panjang rusuk kubus, kita perlu mengetahui volume kubus. Setelah mengetahui volume kubus, kita dapat langsung menghitung panjang rusuk kubus menggunakan rumus s = V.
-
Apa saja aplikasi rumus panjang rusuk kubus?
Rumus panjang rusuk kubus memiliki berbagai aplikasi dalam kehidupan sehari-hari, seperti arsitektur, teknik, dan matematika.
-
Apa satuan panjang rusuk kubus?
Satuan panjang rusuk kubus adalah sama dengan satuan volume kubus. Satuan umum yang digunakan adalah meter (m), sentimeter (cm), atau milimeter (mm).
-
Bagaimana hubungan rumus panjang rusuk kubus dengan diagonal ruang kubus?
Rumus panjang rusuk kubus dapat digunakan untuk menentukan diagonal ruang kubus menggunakan rumus d = s3, di mana d adalah diagonal ruang dan s adalah panjang rusuk kubus.
-
Bagaimana hubungan rumus panjang rusuk kubus dengan luas permukaan kubus?
Rumus panjang rusuk kubus dapat digunakan untuk menentukan luas permukaan kubus menggunakan rumus L = 6s, di mana L adalah luas permukaan dan s adalah panjang rusuk kubus.
Dengan memahami rumus panjang rusuk kubus dan berbagai aspeknya, kita dapat menyelesaikan berbagai soal dan permasalahan yang berkaitan dengan kubus dengan mudah dan akurat.
Artikel Terkait:
- Kubus dan Sifat-sifatnya
- Volume dan Luas Permukaan Kubus
- Diagonal Ruang dan Diagonal Bidang Kubus
Tips Menguasai Rumus Panjang Rusuk Kubus
Rumus panjang rusuk kubus merupakan rumus penting dalam matematika yang memiliki berbagai aplikasi dalam kehidupan sehari-hari. Berikut adalah beberapa tips untuk membantu Anda menguasai rumus panjang rusuk kubus:
Tip 1: Pahami Konsep Volume Kubus
Rumus panjang rusuk kubus berkaitan erat dengan volume kubus. Pastikan Anda memahami konsep volume kubus sebelum mempelajari rumus panjang rusuk kubus.
Tip 2: Gunakan Rumus dengan Benar
Rumus panjang rusuk kubus adalah s = V, di mana s adalah panjang rusuk kubus dan V adalah volume kubus. Hafalkan rumus ini dan gunakan dengan benar.
Tip 3: Perhatikan Satuan
Satuan panjang rusuk kubus harus sama dengan satuan volume kubus. Biasanya menggunakan satuan meter (m), sentimeter (cm), atau milimeter (mm).
Tip 4: Berlatih Soal
Latihlah mengerjakan soal-soal yang berkaitan dengan rumus panjang rusuk kubus. Semakin banyak berlatih, semakin mahir Anda dalam menggunakan rumus ini.
Tip 5: Pahami Aplikasi Rumus
Rumus panjang rusuk kubus memiliki berbagai aplikasi, seperti dalam arsitektur, teknik, dan matematika. Memahami aplikasi ini akan membantu Anda menguasai rumus ini dengan lebih baik.
Dengan mengikuti tips-tips di atas, Anda dapat menguasai rumus panjang rusuk kubus dengan mudah dan efektif.
Kesimpulan
Rumus panjang rusuk kubus merupakan rumus yang penting dan memiliki banyak aplikasi. Dengan memahami konsep yang mendasari dan menerapkan tips-tips yang diberikan, Anda dapat menguasai rumus ini dan menggunakannya untuk menyelesaikan berbagai masalah matematika dan kehidupan sehari-hari.
Kesimpulan
Rumus panjang rusuk kubus merupakan rumus yang sangat penting dan memiliki banyak aplikasi dalam berbagai bidang, seperti arsitektur, teknik, dan matematika. Rumus ini menyatakan bahwa panjang rusuk kubus sama dengan akar pangkat tiga dari volume kubus.
Dengan memahami konsep yang mendasari rumus panjang rusuk kubus dan berbagai aspek yang berkaitan dengannya, kita dapat menggunakan rumus ini secara efektif untuk menyelesaikan berbagai masalah dan perhitungan yang melibatkan kubus. Penguasaan rumus ini sangat penting untuk mengembangkan keterampilan berpikir kritis dan pemecahan masalah dalam matematika dan bidang lainnya.
Youtube Video:
