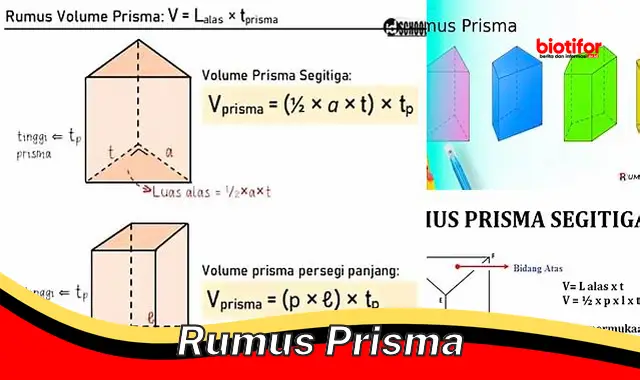
Rumus Prisma adalah rumus yang digunakan untuk menghitung volume dan luas permukaan prisma. Prisma sendiri merupakan bangun ruang yang memiliki dua sisi yang sejajar dan kongruen yang disebut sebagai sisi alas dan sisi atas, serta sisi-sisi lainnya yang berbentuk persegi panjang.
Rumus prisma sangat penting dalam matematika, khususnya dalam bidang geometri. Rumus ini memungkinkan kita untuk menghitung volume dan luas permukaan prisma dengan mudah dan akurat. Selain itu, rumus prisma juga memiliki berbagai aplikasi dalam kehidupan nyata, seperti dalam bidang arsitektur, teknik, dan desain.
Untuk menghitung volume prisma, kita dapat menggunakan rumus V = L x A, di mana V adalah volume, L adalah tinggi prisma, dan A adalah luas alas prisma. Sementara untuk menghitung luas permukaan prisma, kita dapat menggunakan rumus L = 2(Pb + Lb + Pt), di mana L adalah luas permukaan, Pb adalah keliling alas, Lb adalah keliling sisi samping, dan Pt adalah luas sisi atas.
Rumus Prisma
Rumus prisma memegang peranan penting dalam geometri, menyediakan dasar untuk menghitung volume dan luas permukaan prisma.
- Volume Prisma
- Luas Permukaan Prisma
- Panjang Sisi Alas
- Tinggi Prisma
- Keliling Alas
- Keliling Sisi Samping
- Jenis-Jenis Prisma
- Sifat-Sifat Prisma
- Aplikasi Rumus Prisma
- Sejarah Rumus Prisma
Rumus prisma tidak hanya sekedar persamaan matematika, tetapi juga merupakan alat yang ampuh untuk memahami dan menganalisis bentuk tiga dimensi. Dengan memahami rumus ini, kita dapat memperoleh wawasan yang lebih dalam tentang dunia di sekitar kita, dari struktur bangunan hingga objek sehari-hari.
Volume Prisma
Volume prisma merupakan besaran yang menyatakan banyaknya ruang yang ditempati oleh prisma. Volume prisma dapat dihitung menggunakan rumus V = L x A, di mana V adalah volume, L adalah tinggi prisma, dan A adalah luas alas prisma. Rumus ini sangat penting karena memungkinkan kita untuk menentukan kapasitas atau isi sebuah prisma.
Dalam kehidupan nyata, rumus volume prisma memiliki banyak aplikasi penting. Misalnya, dalam bidang arsitektur, rumus ini digunakan untuk menghitung volume ruangan atau bangunan. Dalam bidang teknik, rumus ini digunakan untuk menghitung volume tangki atau wadah. Dalam bidang desain, rumus ini digunakan untuk menghitung volume kemasan atau produk.
Memahami hubungan antara volume prisma dan rumus prisma sangatlah penting karena memungkinkan kita untuk menyelesaikan berbagai masalah matematika dan aplikasi dunia nyata. Dengan memahami rumus ini, kita dapat memperoleh wawasan yang lebih dalam tentang sifat-sifat prisma dan penggunaannya dalam berbagai bidang.
Luas Permukaan Prisma
Luas permukaan prisma merupakan besaran yang menyatakan jumlah luas seluruh permukaan prisma. Luas permukaan prisma dapat dihitung menggunakan rumus L = 2(Pb + Lb + Pt), di mana L adalah luas permukaan, Pb adalah keliling alas, Lb adalah keliling sisi samping, dan Pt adalah luas sisi atas. Rumus ini sangat penting karena memungkinkan kita untuk menentukan luas total permukaan prisma.
-
Keliling Alas
Keliling alas adalah jumlah panjang semua sisi alas prisma. Keliling alas sangat penting dalam menghitung luas permukaan prisma karena merupakan faktor dalam rumus luas permukaan prisma. Dalam kehidupan nyata, keliling alas digunakan dalam berbagai aplikasi, seperti menghitung luas permukaan lantai atau dinding.
-
Keliling Sisi Samping
Keliling sisi samping adalah jumlah panjang semua sisi sisi samping prisma. Keliling sisi samping sangat penting dalam menghitung luas permukaan prisma karena merupakan faktor dalam rumus luas permukaan prisma. Dalam kehidupan nyata, keliling sisi samping digunakan dalam berbagai aplikasi, seperti menghitung luas permukaan kaleng atau pipa.
-
Luas Sisi Atas
Luas sisi atas adalah luas permukaan salah satu sisi atas atau bawah prisma. Luas sisi atas sangat penting dalam menghitung luas permukaan prisma karena merupakan faktor dalam rumus luas permukaan prisma. Dalam kehidupan nyata, luas sisi atas digunakan dalam berbagai aplikasi, seperti menghitung luas permukaan tutup kotak atau meja.
Dengan memahami hubungan antara luas permukaan prisma dan rumus prisma, kita dapat memperoleh wawasan yang lebih dalam tentang sifat-sifat prisma dan penggunaannya dalam berbagai bidang. Rumus luas permukaan prisma memberikan kita alat untuk menghitung luas total permukaan prisma dengan mudah dan akurat.
Panjang Sisi Alas
Panjang sisi alas merupakan salah satu unsur penting dalam rumus prisma. Panjang sisi alas berperan sebagai faktor dalam menghitung keliling alas, yang merupakan salah satu unsur dalam rumus luas permukaan prisma.
Menghitung Keliling Alas
Panjang sisi alas digunakan untuk menghitung keliling alas prisma. Keliling alas merupakan jumlah panjang semua sisi alas prisma. Keliling alas sangat penting dalam menghitung luas permukaan prisma karena merupakan faktor dalam rumus luas permukaan prisma.
Menghitung Luas Permukaan Prisma
Panjang sisi alas juga berperan dalam menghitung luas permukaan prisma. Luas permukaan prisma dihitung menggunakan rumus L = 2(Pb + Lb + Pt), di mana Pb adalah keliling alas. Dengan demikian, panjang sisi alas secara tidak langsung mempengaruhi luas permukaan prisma.
Aplikasi dalam Kehidupan Nyata
Panjang sisi alas prisma memiliki berbagai aplikasi dalam kehidupan nyata. Misalnya, dalam bidang arsitektur, panjang sisi alas digunakan untuk menghitung luas lantai atau dinding. Dalam bidang teknik, panjang sisi alas digunakan untuk menghitung luas permukaan tangki atau wadah. Dalam bidang desain, panjang sisi alas digunakan untuk menghitung luas permukaan kemasan atau produk.
Dengan memahami hubungan antara panjang sisi alas dan rumus prisma, kita dapat memperoleh wawasan yang lebih dalam tentang sifat-sifat prisma dan penggunaannya dalam berbagai bidang. Panjang sisi alas merupakan unsur penting dalam rumus prisma yang memungkinkan kita untuk menghitung berbagai besaran yang berkaitan dengan prisma, seperti keliling alas dan luas permukaan prisma.
Tinggi Prisma
Tinggi prisma merupakan salah satu unsur penting dalam rumus prisma. Tinggi prisma berperan sebagai faktor dalam menghitung volume dan luas permukaan prisma.
-
Menghitung Volume Prisma
Tinggi prisma merupakan unsur penting dalam menghitung volume prisma. Volume prisma dihitung menggunakan rumus V = L x A, di mana L adalah tinggi prisma dan A adalah luas alas prisma. Dengan demikian, tinggi prisma secara langsung mempengaruhi volume prisma.
-
Menghitung Luas Permukaan Prisma
Tinggi prisma juga berperan dalam menghitung luas permukaan prisma. Luas permukaan prisma dihitung menggunakan rumus L = 2(Pb + Lb + Pt), di mana Lb adalah keliling sisi samping prisma. Keliling sisi samping dipengaruhi oleh tinggi prisma, karena tinggi prisma menentukan panjang sisi-sisi samping prisma. Oleh karena itu, tinggi prisma secara tidak langsung mempengaruhi luas permukaan prisma.
-
Aplikasi dalam Kehidupan Nyata
Tinggi prisma memiliki berbagai aplikasi dalam kehidupan nyata. Misalnya, dalam bidang arsitektur, tinggi prisma digunakan untuk menghitung tinggi ruangan atau bangunan. Dalam bidang teknik, tinggi prisma digunakan untuk menghitung tinggi tangki atau wadah. Dalam bidang desain, tinggi prisma digunakan untuk menghitung tinggi kemasan atau produk.
Dengan memahami hubungan antara tinggi prisma dan rumus prisma, kita dapat memperoleh wawasan yang lebih dalam tentang sifat-sifat prisma dan penggunaannya dalam berbagai bidang. Tinggi prisma merupakan unsur penting dalam rumus prisma yang memungkinkan kita untuk menghitung berbagai besaran yang berkaitan dengan prisma, seperti volume dan luas permukaan prisma.
Keliling Alas
Keliling alas merupakan besaran yang menyatakan panjang seluruh sisi alas prisma. Keliling alas memegang peranan penting dalam rumus prisma, khususnya dalam menghitung luas permukaan prisma.
Dalam rumus L = 2(Pb + Lb + Pt), di mana L adalah luas permukaan, Pb adalah keliling alas, Lb adalah keliling sisi samping, dan Pt adalah luas sisi atas, keliling alas menjadi salah satu faktor penentu luas permukaan prisma. Semakin besar keliling alas, maka semakin besar pula luas permukaan prisma.
Keliling alas digunakan dalam berbagai aplikasi kehidupan nyata, seperti menghitung luas permukaan lantai atau dinding dalam arsitektur, menghitung luas permukaan tangki atau wadah dalam teknik, dan menghitung luas permukaan kemasan atau produk dalam desain.
Memahami hubungan antara keliling alas dan rumus prisma sangat penting karena memungkinkan kita untuk menghitung luas permukaan prisma dengan mudah dan akurat. Dengan memahami konsep ini, kita dapat memperoleh wawasan yang lebih dalam tentang sifat-sifat prisma dan penggunaannya dalam berbagai bidang.
Keliling Sisi Samping
Keliling sisi samping merupakan besaran yang menyatakan panjang seluruh sisi samping prisma. Keliling sisi samping memegang peranan penting dalam rumus prisma, khususnya dalam menghitung luas permukaan prisma.
-
Menghitung Luas Permukaan Prisma
Keliling sisi samping merupakan salah satu faktor dalam menghitung luas permukaan prisma. Rumus luas permukaan prisma adalah L = 2(Pb + Lb + Pt), di mana L adalah luas permukaan, Pb adalah keliling alas, Lb adalah keliling sisi samping, dan Pt adalah luas sisi atas. Semakin besar keliling sisi samping, maka semakin besar pula luas permukaan prisma.
-
Aplikasi dalam Kehidupan Nyata
Keliling sisi samping digunakan dalam berbagai aplikasi kehidupan nyata, seperti menghitung luas permukaan kaleng atau pipa dalam teknik, menghitung luas permukaan kemasan atau produk dalam desain, dan menghitung luas permukaan dinding atau pagar dalam arsitektur.
Memahami hubungan antara keliling sisi samping dan rumus prisma sangat penting karena memungkinkan kita untuk menghitung luas permukaan prisma dengan mudah dan akurat. Dengan memahami konsep ini, kita dapat memperoleh wawasan yang lebih dalam tentang sifat-sifat prisma dan penggunaannya dalam berbagai bidang.
Jenis-Jenis Prisma
Jenis-jenis prisma merupakan bagian penting dalam memahami rumus prisma. Jenis prisma menentukan rumus yang digunakan untuk menghitung volume dan luas permukaan prisma.
Ada beberapa jenis prisma yang umum ditemukan, antara lain:
- Prisma Segitiga
- Prisma Segiempat
- Prisma Segi Lima
- Prisma Segi Enam
Setiap jenis prisma memiliki rumus yang berbeda untuk menghitung volume dan luas permukaannya. Misalnya, untuk menghitung volume prisma segitiga, digunakan rumus V = 1/2 x Luas alas x Tinggi. Sedangkan untuk menghitung luas permukaan prisma segi empat, digunakan rumus L = 2(Pb + Lb + Pt), di mana Pb adalah keliling alas, Lb adalah keliling sisi samping, dan Pt adalah luas sisi atas.
Memahami jenis-jenis prisma dan rumus yang sesuai sangat penting dalam menyelesaikan masalah yang berkaitan dengan prisma. Dengan memahami konsep ini, kita dapat memperoleh wawasan yang lebih dalam tentang sifat-sifat prisma dan penggunaannya dalam berbagai bidang.
Sifat-Sifat Prisma
Sifat-sifat prisma merupakan karakteristik yang melekat pada prisma. Sifat-sifat ini sangat penting dalam memahami rumus prisma karena menjadi dasar dalam pengembangan rumus tersebut.
Salah satu sifat penting prisma adalah memiliki dua sisi yang sejajar dan kongruen yang disebut sisi alas dan sisi atas. Sisi-sisi lainnya berbentuk persegi panjang. Sifat ini menjadi dasar dalam menentukan luas sisi alas dan tinggi prisma, yang merupakan faktor penting dalam rumus volume dan luas permukaan prisma.
Sifat penting lainnya dari prisma adalah rusuk-rusuknya yang sejajar dan sama panjang. Sifat ini menjadi dasar dalam menentukan keliling sisi samping prisma, yang juga merupakan faktor penting dalam rumus luas permukaan prisma.
Memahami sifat-sifat prisma dan hubungannya dengan rumus prisma sangat penting dalam menyelesaikan masalah yang berkaitan dengan prisma. Dengan memahami konsep ini, kita dapat memperoleh wawasan yang lebih dalam tentang sifat-sifat prisma dan penggunaannya dalam berbagai bidang, seperti arsitektur, teknik, dan desain.
Aplikasi Rumus Prisma
Rumus prisma merupakan alat penting untuk menyelesaikan berbagai masalah matematika dan aplikasi dunia nyata yang melibatkan prisma. Rumus ini memungkinkan kita menghitung volume dan luas permukaan prisma dengan mudah dan akurat. Berikut adalah beberapa aplikasi rumus prisma:
-
Arsitektur
Dalam arsitektur, rumus prisma digunakan untuk menghitung volume dan luas permukaan bangunan dan ruangan. Misalnya, arsitek menggunakan rumus prisma untuk menghitung volume ruangan untuk menentukan kebutuhan pendingin udara atau luas permukaan dinding untuk menghitung kebutuhan cat.
-
Teknik
Dalam teknik, rumus prisma digunakan untuk menghitung volume dan luas permukaan tangki, wadah, dan struktur lainnya. Misalnya, insinyur menggunakan rumus prisma untuk menghitung volume tangki air untuk menentukan kapasitasnya atau luas permukaan pipa untuk menghitung kebutuhan insulasi.
-
Desain
Dalam desain, rumus prisma digunakan untuk menghitung volume dan luas permukaan kemasan, produk, dan benda lainnya. Misalnya, desainer menggunakan rumus prisma untuk menghitung volume kemasan untuk menentukan kapasitasnya atau luas permukaan produk untuk menghitung kebutuhan bahan.
-
Matematika
Dalam matematika, rumus prisma merupakan bagian penting dari geometri. Rumus ini digunakan untuk memecahkan berbagai masalah geometri yang melibatkan prisma, seperti mencari volume dan luas permukaan prisma dengan bentuk dan ukuran yang berbeda.
Dengan memahami rumus prisma dan aplikasinya, kita dapat memperoleh wawasan yang lebih dalam tentang sifat-sifat prisma dan penggunaannya dalam berbagai bidang. Rumus ini merupakan alat yang ampuh untuk menyelesaikan masalah matematika dan aplikasi dunia nyata yang melibatkan prisma.
Sejarah Rumus Prisma
Sejarah rumus prisma tidak terlepas dari perkembangan matematika itu sendiri. Konsep prisma dan volumenya pertama kali dipelajari oleh matematikawan Yunani kuno seperti Euclid dan Archimedes. Euclid, dalam bukunya “Elements”, mendefinisikan prisma sebagai bangun ruang yang memiliki dua sisi sejajar dan kongruen, serta sisi-sisi lainnya berbentuk persegi panjang. Archimedes, dalam karyanya “On the Sphere and the Cylinder”, mengembangkan metode untuk menghitung volume prisma, yang menjadi dasar bagi rumus prisma yang kita gunakan saat ini.
Seiring berjalannya waktu, rumus prisma disempurnakan dan digeneralisasikan oleh matematikawan lainnya. Pada abad ke-17, Ren Descartes memperkenalkan sistem koordinat Cartesian, yang memungkinkan rumus prisma dinyatakan dalam bentuk aljabar. Pada abad ke-19, Carl Friedrich Gauss dan Bernhard Riemann mengembangkan konsep kalkulus vektor, yang memperluas jangkauan rumus prisma ke dimensi yang lebih tinggi.
Memahami sejarah rumus prisma sangat penting karena memberikan konteks dan pemahaman yang lebih dalam tentang perkembangan matematika. Hal ini juga menunjukkan bahwa rumus prisma yang kita gunakan saat ini merupakan hasil dari akumulasi pengetahuan dan kerja keras para matematikawan selama berabad-abad. Dengan menghargai sejarahnya, kita dapat lebih menghargai kekuatan dan kegunaan rumus prisma dalam memecahkan masalah matematika dan aplikasi dunia nyata.
FAQ Rumus Prisma
Bagian ini menyajikan tanya jawab umum seputar rumus prisma yang akan membantu Anda memahami konsep ini secara lebih komprehensif.
Pertanyaan 1: Apa saja jenis-jenis prisma dan bagaimana rumus untuk menghitung volumenya?
Jawaban: Jenis-jenis prisma antara lain prisma segitiga, segiempat, segi lima, dan segi enam. Rumus volume untuk masing-masing jenis prisma berbeda. Untuk prisma segitiga, rumusnya adalah 1/2 x Luas alas x Tinggi. Untuk prisma lainnya, rumusnya adalah Luas alas x Tinggi.
Dengan memahami FAQ ini, diharapkan Anda dapat memiliki pemahaman yang lebih baik tentang rumus prisma dan aplikasinya. Jika Anda memiliki pertanyaan lebih lanjut, jangan ragu untuk berkonsultasi dengan sumber lain atau mencari bantuan dari ahli matematika.
Beralih ke bagian selanjutnya untuk eksplorasi lebih mendalam tentang rumus prisma.
Tips Mengenai Rumus Prisma
Rumus prisma sangat penting dalam geometri karena memungkinkan kita menghitung volume dan luas permukaan prisma. Berikut adalah beberapa tips untuk membantu Anda memahami dan menggunakan rumus prisma secara efektif:
Tip 1: Pahami Konsep Dasar Prisma
Sebelum mempelajari rumus prisma, penting untuk memahami konsep dasar prisma. Prisma adalah bangun ruang yang memiliki dua sisi yang sejajar dan kongruen (disebut sisi alas dan sisi atas) serta sisi-sisi lainnya berbentuk persegi panjang.
Tip 2: Hafalkan Rumus-Rumus Penting
Ada beberapa rumus prisma yang penting untuk dihafalkan, yaitu rumus volume (V = L x A) dan rumus luas permukaan (L = 2(Pb + Lb + Pt)). L adalah tinggi prisma, A adalah luas alas, Pb adalah keliling alas, Lb adalah keliling sisi samping, dan Pt adalah luas sisi atas.
Tip 3: Latih Soal-Soal
Cara terbaik untuk menguasai rumus prisma adalah dengan berlatih soal sebanyak-banyaknya. Carilah soal-soal latihan dari buku teks, soal ujian, atau sumber daring.
Tip 4: Visualisasikan Prisma
Saat mengerjakan soal prisma, cobalah untuk memvisualisasikan prisma yang dimaksud. Hal ini akan membantu Anda memahami soal dengan lebih baik dan menemukan rumus yang tepat.
Tip 5: Gunakan Kalkulator Secara Bijak
Kalkulator dapat membantu Anda menghitung nilai numerik dengan cepat dan akurat. Namun, jangan terlalu bergantung pada kalkulator. Pastikan Anda memahami konsep dan rumus yang digunakan.
Dengan mengikuti tips ini, Anda akan dapat memahami dan menggunakan rumus prisma dengan lebih baik. Rumus-rumus ini merupakan alat yang ampuh untuk memecahkan masalah geometri dan aplikasi dunia nyata yang melibatkan prisma.
Kesimpulan Rumus Prisma
Rumus prisma merupakan alat penting dalam geometri untuk menghitung volume dan luas permukaan prisma. Rumus-rumus ini memiliki berbagai aplikasi dalam kehidupan nyata, seperti arsitektur, teknik, dan desain. Memahami rumus prisma akan memberikan wawasan yang lebih dalam tentang sifat-sifat prisma dan penggunaannya dalam berbagai bidang.
Dalam artikel ini, kita telah mengeksplorasi berbagai aspek rumus prisma, termasuk jenis-jenis prisma, sifat-sifatnya, dan aplikasinya. Kita juga telah membahas sejarah rumus prisma dan memberikan tips untuk memahami dan menggunakan rumus tersebut secara efektif.
Youtube Video:
