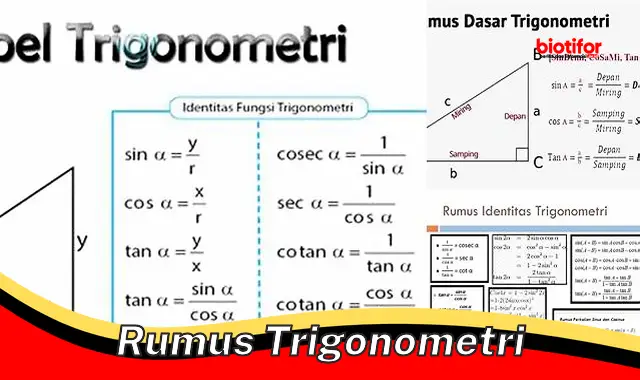
Rumus trigonometri adalah persamaan matematika yang menghubungkan sisi dan sudut segitiga siku-siku. Rumus-rumus ini digunakan untuk menghitung sisi atau sudut yang tidak diketahui dari sebuah segitiga jika diketahui nilai sisi atau sudut lainnya.
Rumus trigonometri sangat penting dalam berbagai bidang, seperti navigasi, teknik, dan astronomi. Dalam navigasi, rumus trigonometri digunakan untuk menghitung jarak dan arah ke suatu tujuan. Dalam teknik, rumus trigonometri digunakan untuk menghitung beban dan tekanan pada struktur. Dalam astronomi, rumus trigonometri digunakan untuk menghitung jarak dan posisi benda-benda langit.
Rumus trigonometri pertama kali dikembangkan oleh matematikawan Yunani Kuno sekitar abad ke-3 SM. Rumus-rumus ini kemudian disempurnakan oleh matematikawan India dan Arab pada Abad Pertengahan. Rumus trigonometri modern dikembangkan pada abad ke-16 oleh matematikawan Eropa.
Rumus Trigonometri
Rumus trigonometri adalah persamaan matematika yang digunakan untuk menghitung sisi dan sudut segitiga siku-siku. Rumus-rumus ini sangat penting dalam berbagai bidang, seperti navigasi, teknik, dan astronomi.
- Definisi
- Jenis-jenis
- Aplikasi
- Sejarah
- Tokoh-tokoh penting
- Contoh soal
- Tabel rumus
- Kalkulator online
- Perangkat lunak
Rumus trigonometri dapat digunakan untuk menghitung panjang sisi segitiga jika diketahui panjang sisi lainnya dan sudut yang mengapitnya. Rumus-rumus ini juga dapat digunakan untuk menghitung besar sudut segitiga jika diketahui panjang sisi-sisinya. Selain itu, rumus trigonometri juga dapat digunakan untuk menyelesaikan berbagai masalah lainnya, seperti menentukan jarak dan arah suatu benda.
Definisi
Definisi adalah suatu pernyataan yang menjelaskan makna suatu istilah atau konsep. Definisi sangat penting dalam matematika, karena memungkinkan kita untuk memahami konsep-konsep matematika dengan jelas dan tepat.
Rumus trigonometri adalah persamaan matematika yang digunakan untuk menghitung sisi dan sudut segitiga siku-siku. Rumus-rumus ini sangat penting dalam berbagai bidang, seperti navigasi, teknik, dan astronomi.
Definisi rumus trigonometri sangat penting karena memungkinkan kita untuk memahami konsep rumus trigonometri dengan jelas dan tepat. Definisi ini juga memungkinkan kita untuk menggunakan rumus trigonometri dengan benar untuk menyelesaikan masalah.
Sebagai contoh, rumus trigonometri sinus didefinisikan sebagai perbandingan antara panjang sisi depan dan panjang sisi miring sebuah segitiga siku-siku. Definisi ini memungkinkan kita untuk memahami bahwa sinus suatu sudut adalah ukuran relatif dari sisi depan segitiga siku-siku.
Definisi rumus trigonometri juga sangat penting untuk pengembangan matematika. Definisi yang jelas dan tepat memungkinkan matematikawan untuk membangun teori matematika yang konsisten dan logis.
Jenis-jenis
Rumus trigonometri dapat dibedakan menjadi beberapa jenis, yaitu:
- Rumus sinus
- Rumus kosinus
- Rumus tangen
- Rumus kotangen
- Rumus sekan
- Rumus kosekan
Setiap jenis rumus trigonometri memiliki fungsi yang berbeda-beda. Misalnya, rumus sinus digunakan untuk menghitung panjang sisi depan segitiga siku-siku jika diketahui panjang sisi miring dan besar sudut yang mengapitnya. Sedangkan rumus kosinus digunakan untuk menghitung panjang sisi miring segitiga siku-siku jika diketahui panjang kedua sisi lainnya.
Jenis-jenis rumus trigonometri sangat penting dipahami karena masing-masing jenis memiliki fungsi yang berbeda-beda. Dengan memahami jenis-jenis rumus trigonometri, kita dapat menggunakan rumus yang tepat untuk menyelesaikan masalah yang dihadapi.
Aplikasi
Rumus trigonometri memiliki banyak aplikasi dalam berbagai bidang, seperti navigasi, teknik, dan astronomi. Dalam navigasi, rumus trigonometri digunakan untuk menghitung jarak dan arah ke suatu tujuan. Dalam teknik, rumus trigonometri digunakan untuk menghitung beban dan tekanan pada struktur. Dalam astronomi, rumus trigonometri digunakan untuk menghitung jarak dan posisi benda-benda langit.
Salah satu aplikasi penting rumus trigonometri adalah dalam bidang teknik sipil. Rumus trigonometri digunakan untuk menghitung beban dan tekanan pada struktur bangunan, seperti jembatan dan gedung. Dengan menggunakan rumus trigonometri, insinyur dapat memastikan bahwa struktur bangunan aman dan tidak akan runtuh.
Aplikasi lain dari rumus trigonometri adalah dalam bidang navigasi. Rumus trigonometri digunakan untuk menghitung jarak dan arah ke suatu tujuan. Dengan menggunakan rumus trigonometri, pelaut dan pilot dapat menentukan lokasi mereka dan merencanakan jalur perjalanan mereka.
Sejarah
Sejarah rumus trigonometri sangat panjang dan menarik, yang dimulai pada zaman dahulu kala oleh para matematikawan Yunani. Rumus-rumus trigonometri pertama kali dikembangkan oleh matematikawan Yunani kuno seperti Hipparchus dan Ptolemy pada abad ke-2 SM. Mereka menggunakan rumus-rumus ini untuk menghitung jarak ke bulan dan matahari, serta untuk menyelesaikan masalah navigasi.
-
Pengaruh matematikawan India
Matematikawan India juga memberikan kontribusi yang signifikan terhadap perkembangan rumus trigonometri. Pada abad ke-5 Masehi, matematikawan India Aryabhata mengembangkan sinus setengah sudut dan kosinus setengah sudut, serta rumus-rumus untuk menghitung sinus dan kosinus dari sudut yang lebih besar dari 90 derajat.
-
Pengaruh matematikawan Arab
Matematikawan Arab juga memainkan peran penting dalam pengembangan rumus trigonometri. Pada abad ke-9 Masehi, matematikawan Arab Al-Khwarizmi mengembangkan tangen dan kotangen, serta rumus-rumus untuk menyelesaikan persamaan trigonometri.
-
Pengaruh matematikawan Eropa
Pada abad ke-16, matematikawan Eropa seperti Regiomontanus dan Franois Vite mengembangkan rumus-rumus trigonometri modern yang kita gunakan sampai sekarang. Mereka juga mengembangkan tabel trigonometri, yang memudahkan perhitungan trigonometri.
-
Pengaruh kalkulus
Pada abad ke-17, kalkulus ditemukan oleh Isaac Newton dan Gottfried Leibniz. Kalkulus memungkinkan matematikawan untuk mengembangkan rumus-rumus trigonometri yang lebih canggih, seperti rumus penjumlahan dan selisih sudut.
Sejarah rumus trigonometri menunjukkan bahwa rumus-rumus ini telah dikembangkan selama berabad-abad oleh matematikawan dari berbagai budaya yang berbeda. Rumus-rumus ini sangat penting untuk navigasi, astronomi, dan bidang lainnya, dan terus digunakan hingga sekarang.
Tokoh-tokoh penting
Tokoh-tokoh penting dalam pengembangan rumus trigonometri adalah orang-orang yang telah membuat kontribusi signifikan terhadap bidang ini. Kontribusi mereka mencakup pengembangan rumus-rumus baru, penyempurnaan rumus-rumus yang sudah ada, dan penerapan rumus trigonometri ke bidang-bidang baru.
-
Hipparchus
Hipparchus adalah seorang matematikawan dan astronom Yunani yang hidup pada abad ke-2 SM. Dia dikenal sebagai bapak trigonometri karena kontribusinya yang signifikan terhadap bidang ini. Hipparchus mengembangkan tabel trigonometri pertama, yang berisi nilai-nilai sinus dan kosinus untuk berbagai sudut. Dia juga mengembangkan rumus untuk menghitung jarak ke bulan dan matahari.
-
Ptolemy
Ptolemy adalah seorang matematikawan dan astronom Yunani yang hidup pada abad ke-2 Masehi. Dia dikenal karena karyanya pada bidang astronomi, geografi, dan trigonometri. Ptolemy mengembangkan rumus-rumus trigonometri baru, termasuk rumus untuk menghitung sinus dan kosinus dari sudut yang lebih besar dari 90 derajat.
-
Aryabhata
Aryabhata adalah seorang matematikawan dan astronom India yang hidup pada abad ke-5 Masehi. Dia dikenal karena karyanya pada bidang matematika, astronomi, dan fisika. Aryabhata mengembangkan sinus setengah sudut dan kosinus setengah sudut, serta rumus-rumus untuk menghitung sinus dan kosinus dari sudut yang lebih besar dari 90 derajat.
-
Al-Khwarizmi
Al-Khwarizmi adalah seorang matematikawan dan astronom Persia yang hidup pada abad ke-9 Masehi. Dia dikenal karena karyanya pada bidang aljabar, trigonometri, dan astronomi. Al-Khwarizmi mengembangkan tangen dan kotangen, serta rumus-rumus untuk menyelesaikan persamaan trigonometri.
Tokoh-tokoh penting ini telah memberikan kontribusi yang signifikan terhadap pengembangan rumus trigonometri. Kontribusi mereka telah memungkinkan kita untuk memahami dan menggunakan rumus trigonometri untuk menyelesaikan berbagai masalah di berbagai bidang, termasuk navigasi, astronomi, dan teknik.
Contoh soal
Contoh soal trigonometri adalah soal-soal yang berkaitan dengan penerapan rumus trigonometri untuk menyelesaikan permasalahan yang melibatkan besaran sudut dan sisi segitiga siku-siku. Soal-soal ini digunakan untuk menguji pemahaman siswa terhadap konsep trigonometri dan kemampuan mereka dalam menerapkan rumus-rumus trigonometri.
-
Menghitung panjang sisi segitiga
Contoh soal ini mengharuskan siswa untuk menggunakan rumus trigonometri untuk menghitung panjang sisi segitiga yang belum diketahui, berdasarkan panjang sisi lain dan besar sudut yang diketahui.
-
Menghitung besar sudut segitiga
Contoh soal ini mengharuskan siswa untuk menggunakan rumus trigonometri untuk menghitung besar sudut segitiga yang belum diketahui, berdasarkan panjang sisi-sisinya yang diketahui.
-
Menentukan arah resultan gaya
Contoh soal ini mengharuskan siswa untuk menggunakan rumus trigonometri untuk menentukan arah resultan gaya yang bekerja pada suatu benda, berdasarkan besar dan arah gaya-gaya penyusunnya.
-
Menghitung jarak benda dengan menggunakan trigonometri
Contoh soal ini mengharuskan siswa untuk menggunakan rumus trigonometri untuk menghitung jarak suatu benda dari titik pengamat, berdasarkan sudut elevasi atau sudut depresi yang diketahui.
Contoh soal trigonometri sangat penting untuk melatih pemahaman siswa terhadap konsep trigonometri dan meningkatkan kemampuan mereka dalam menerapkan rumus-rumus trigonometri pada permasalahan nyata. Dengan mengerjakan contoh soal trigonometri, siswa dapat memperkuat pemahaman mereka tentang hubungan antara sudut dan sisi segitiga siku-siku.
Tabel Rumus
Tabel rumus adalah kumpulan rumus-rumus yang disusun secara sistematis dan rapi sehingga mudah untuk ditemukan dan digunakan. Tabel rumus trigonometri berisi daftar rumus-rumus trigonometri yang umum digunakan, seperti rumus sinus, kosinus, tangen, kotangen, sekan, dan kosekan.
-
Fungsi Tabel Rumus
Tabel rumus trigonometri sangat penting untuk mempermudah dan mempercepat penyelesaian masalah trigonometri. Dengan adanya tabel rumus, pengguna tidak perlu menghafal semua rumus trigonometri, sehingga dapat menghemat waktu dan tenaga.
-
Contoh Penggunaan Tabel Rumus
Sebagai contoh, jika pengguna ingin menghitung nilai sinus dari suatu sudut, pengguna cukup mencari rumus sinus pada tabel rumus dan kemudian memasukkan nilai sudut tersebut ke dalam rumus. Hasilnya akan langsung diperoleh tanpa harus mengingat rumus sinus secara hafalan.
-
Jenis-jenis Tabel Rumus
Selain tabel rumus trigonometri, terdapat juga tabel rumus untuk bidang matematika lainnya, seperti tabel rumus aljabar, kalkulus, dan statistika. Setiap tabel rumus berisi kumpulan rumus-rumus yang umum digunakan pada bidang matematika tersebut.
-
Cara Menggunakan Tabel Rumus
Untuk menggunakan tabel rumus, pengguna cukup mencari topik atau rumus yang ingin digunakan. Setelah ditemukan, pengguna dapat langsung memasukkan nilai-nilai yang diketahui ke dalam rumus dan menghitung hasilnya. Tabel rumus juga biasanya dilengkapi dengan contoh-contoh soal yang dapat membantu pengguna memahami cara penggunaan tabel rumus.
Tabel rumus trigonometri merupakan alat bantu yang sangat penting dalam mempelajari dan menyelesaikan masalah trigonometri. Dengan adanya tabel rumus, pengguna dapat menghemat waktu dan tenaga, serta mempermudah proses penyelesaian masalah trigonometri.
Kalkulator Online
Kalkulator online adalah alat yang dapat digunakan untuk menyelesaikan perhitungan trigonometri dengan cepat dan mudah. Kalkulator ini tersedia secara gratis di internet, dan dapat digunakan untuk menyelesaikan berbagai jenis perhitungan trigonometri, seperti menghitung nilai sinus, kosinus, tangen, kotangen, sekan, dan kosekan suatu sudut.
-
Komponen Kalkulator Online
Kalkulator online trigonometri biasanya memiliki antarmuka yang sederhana dan mudah digunakan. Pengguna hanya perlu memasukkan nilai sudut yang ingin dihitung, dan kalkulator akan secara otomatis menghitung nilai trigonometrinya. Beberapa kalkulator online juga menyediakan fitur tambahan, seperti kemampuan untuk menghitung nilai trigonometri untuk beberapa sudut sekaligus, atau untuk mengonversi antara derajat dan radian.
-
Contoh Penggunaan Kalkulator Online
Kalkulator online trigonometri dapat digunakan untuk menyelesaikan berbagai jenis masalah trigonometri. Misalnya, kalkulator ini dapat digunakan untuk menghitung tinggi sebuah bangunan, jarak ke suatu objek, atau sudut suatu segitiga. Kalkulator ini juga dapat digunakan untuk menyelesaikan persamaan trigonometri.
-
Implikasi Kalkulator Online
Kalkulator online trigonometri memiliki beberapa implikasi penting. Pertama, kalkulator ini dapat menghemat banyak waktu dan tenaga. Kedua, kalkulator ini dapat membantu pengguna untuk menghindari kesalahan perhitungan. Ketiga, kalkulator ini dapat membuat pembelajaran trigonometri lebih mudah dan menyenangkan.
-
Perbandingan dengan Metode Tradisional
Kalkulator online trigonometri menawarkan beberapa keuntungan dibandingkan dengan metode tradisional untuk menyelesaikan perhitungan trigonometri. Pertama, kalkulator online lebih cepat dan mudah digunakan. Kedua, kalkulator online lebih akurat. Ketiga, kalkulator online lebih mudah diakses.
Kalkulator online trigonometri adalah alat yang sangat berguna untuk menyelesaikan perhitungan trigonometri. Kalkulator ini dapat menghemat waktu dan tenaga, membantu pengguna untuk menghindari kesalahan perhitungan, dan membuat pembelajaran trigonometri lebih mudah dan menyenangkan.
Perangkat Lunak
Dalam dunia matematika, perangkat lunak memainkan peran penting untuk memudahkan proses perhitungan dan penyelesaian masalah, termasuk dalam hal penerapan rumus trigonometri. Berikut ini adalah beberapa keterkaitan antara perangkat lunak dan rumus trigonometri:
-
Kalkulator Ilmiah
Kalkulator ilmiah adalah perangkat lunak yang dirancang untuk melakukan berbagai macam perhitungan, termasuk perhitungan trigonometri. Perangkat lunak ini menyediakan fungsi-fungsi seperti menghitung nilai sinus, kosinus, tangen, dan fungsi trigonometri lainnya untuk sudut tertentu.
-
Spreadsheet
Spreadsheet seperti Microsoft Excel atau Google Sheets dapat digunakan untuk melakukan perhitungan trigonometri yang lebih kompleks. Pengguna dapat memasukkan rumus trigonometri ke dalam sel spreadsheet dan kemudian memasukkan nilai sudut yang ingin dihitung. Spreadsheet akan secara otomatis menghitung dan menampilkan hasilnya.
-
Sistem Aljabar Komputer (CAS)
CAS seperti Wolfram Alpha atau MATLAB menyediakan fungsionalitas yang lebih canggih untuk perhitungan trigonometri. Selain dapat menghitung nilai fungsi trigonometri, CAS juga dapat menyelesaikan persamaan trigonometri, menplot grafik fungsi trigonometri, dan melakukan operasi matematika lainnya yang terkait dengan trigonometri.
-
Aplikasi Seluler
Ada banyak aplikasi seluler yang tersedia untuk menghitung fungsi trigonometri dan menyelesaikan masalah trigonometri. Aplikasi ini biasanya menyediakan antarmuka yang ramah pengguna dan dapat digunakan untuk menghitung nilai trigonometri dengan cepat dan mudah.
Penggunaan perangkat lunak untuk menghitung rumus trigonometri sangat bermanfaat karena dapat menghemat waktu dan tenaga, mengurangi kesalahan perhitungan, dan memungkinkan pengguna untuk fokus pada aspek pemecahan masalah yang lebih konseptual.
Pertanyaan Umum tentang Rumus Trigonometri
Rumus trigonometri adalah persamaan matematika yang digunakan untuk menghitung sisi dan sudut segitiga siku-siku. Rumus-rumus ini sangat penting dalam berbagai bidang, seperti navigasi, teknik, dan astronomi.
Berikut adalah beberapa pertanyaan umum tentang rumus trigonometri:
Pertanyaan 1: Apa saja rumus trigonometri yang paling umum digunakan?
Jawaban: Rumus trigonometri yang paling umum digunakan adalah sinus, kosinus, tangen, kotangen, sekan, dan kosekan. Rumus-rumus ini digunakan untuk menghitung panjang sisi dan besar sudut segitiga siku-siku.
Pertanyaan 2: Bagaimana cara menggunakan rumus trigonometri?
Jawaban: Untuk menggunakan rumus trigonometri, kita perlu mengetahui nilai salah satu sisi atau sudut segitiga siku-siku. Kemudian, kita dapat menggunakan rumus yang sesuai untuk menghitung nilai sisi atau sudut yang belum diketahui.
Pertanyaan 3: Apa saja aplikasi rumus trigonometri?
Jawaban: Rumus trigonometri memiliki banyak aplikasi dalam berbagai bidang, seperti navigasi, teknik, dan astronomi. Dalam navigasi, rumus trigonometri digunakan untuk menghitung jarak dan arah ke suatu tujuan. Dalam teknik, rumus trigonometri digunakan untuk menghitung beban dan tekanan pada struktur. Dalam astronomi, rumus trigonometri digunakan untuk menghitung jarak dan posisi benda-benda langit.
Pertanyaan 4: Apakah rumus trigonometri sulit untuk dipelajari?
Jawaban: Rumus trigonometri tidak sulit untuk dipelajari jika kita memahami konsep dasarnya. Kita perlu memahami konsep segitiga siku-siku, perbandingan trigonometri, dan rumus-rumus trigonometri.
Pertanyaan 5: Di mana saya dapat menemukan sumber daya untuk mempelajari rumus trigonometri?
Jawaban: Ada banyak sumber daya yang tersedia untuk mempelajari rumus trigonometri, seperti buku teks, situs web, dan video tutorial. Kita juga dapat mencari bantuan dari guru atau tutor jika kita mengalami kesulitan.
Rumus trigonometri adalah alat yang sangat penting dalam berbagai bidang. Dengan memahami dan menggunakan rumus trigonometri dengan benar, kita dapat menyelesaikan masalah yang berkaitan dengan segitiga siku-siku dan menerapkannya dalam kehidupan nyata.
Lanjut ke bagian berikutnya: Penerapan Rumus Trigonometri
Tips Menguasai Rumus Trigonometri
Trigonometri merupakan cabang matematika yang mempelajari hubungan antara sisi dan sudut segitiga. Mempelajari rumus trigonometri sangat penting karena memiliki banyak aplikasi dalam berbagai bidang, seperti navigasi, teknik, dan astronomi.
Berikut adalah beberapa tips untuk menguasai rumus trigonometri:
Tip 1: Pahami Konsep Dasar
Sebelum mempelajari rumus trigonometri, pastikan untuk memahami konsep dasar trigonometri, seperti definisi sinus, kosinus, dan tangen. Memahami konsep dasar akan memudahkan Anda dalam memahami dan menerapkan rumus trigonometri.
Tip 2: Hafalkan Rumus-rumus Dasar
Ada beberapa rumus trigonometri dasar yang perlu Anda hafalkan, seperti rumus sinus, kosinus, dan tangen. Rumus-rumus ini akan menjadi dasar untuk menyelesaikan berbagai soal trigonometri.
Tip 3: Latihan Soal Secara Teratur
Latihan soal secara teratur sangat penting untuk menguasai rumus trigonometri. Semakin banyak soal yang Anda kerjakan, semakin terbiasa Anda dalam menerapkan rumus trigonometri dan menyelesaikan masalah.
Tip 4: Gunakan Kalkulator Ilmiah
Kalkulator ilmiah dapat membantu Anda menghitung nilai trigonometri dengan cepat dan akurat. Namun, pastikan Anda memahami konsep dasar trigonometri sebelum menggunakan kalkulator.
Tip 5: Jangan Menyerah
Trigonometri mungkin terlihat sulit pada awalnya, tetapi jangan menyerah. Dengan usaha dan ketekunan, Anda pasti bisa menguasai rumus trigonometri dan menerapkannya untuk menyelesaikan masalah-masalah dalam kehidupan nyata.
Menguasai rumus trigonometri membutuhkan waktu dan usaha. Namun, dengan mengikuti tips-tips di atas, Anda dapat mempercepat proses belajar dan menguasai trigonometri dengan lebih efektif.
Lanjutkan membaca: Penerapan Rumus Trigonometri
Kesimpulan
Rumus trigonometri merupakan bagian penting dari matematika yang memiliki banyak aplikasi dalam berbagai bidang, seperti navigasi, teknik, dan astronomi. Rumus-rumus ini digunakan untuk menghitung sisi dan sudut segitiga siku-siku, serta menyelesaikan berbagai masalah yang melibatkan besaran sudut dan jarak.
Dalam artikel ini, kita telah membahas berbagai aspek rumus trigonometri, mulai dari definisi, jenis-jenis, hingga aplikasinya. Kita juga telah mempelajari tokoh-tokoh penting dalam pengembangan rumus trigonometri, serta sumber daya yang tersedia untuk mempelajarinya.
Dengan memahami dan menguasai rumus trigonometri, kita dapat menyelesaikan masalah-masalah yang kompleks dan menerapkannya dalam berbagai bidang kehidupan nyata. Oleh karena itu, sangat penting untuk terus mempelajari dan memperdalam pengetahuan kita tentang trigonometri.
Youtube Video:
