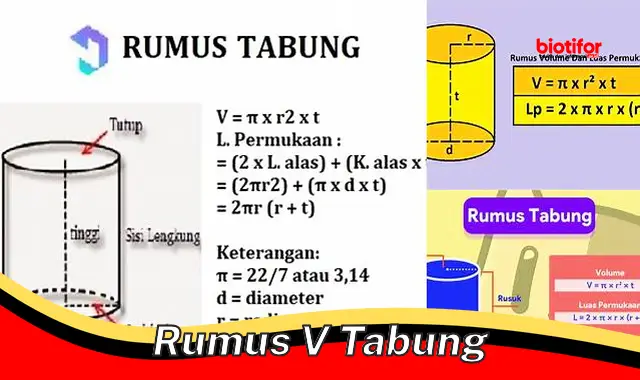
Rumus Sederhana dan Akurat untuk Menghitung Volume Tabung

Rumus volume tabung adalah persamaan matematika yang digunakan untuk menghitung volume benda berbentuk tabung. Rumus tersebut dinyatakan sebagai:

V = rt

di mana:

V adalah volume tabung dalam satuan kubik
adalah konstanta matematika yang nilainya sekitar 3,14
r adalah jari-jari alas tabung dalam satuan panjang
t adalah tinggi tabung dalam satuan panjang

Rumus volume tabung sangat penting dalam berbagai bidang, seperti teknik, fisika, dan matematika. Rumus ini digunakan untuk menghitung volume benda-benda berbentuk tabung, seperti pipa, kaleng, dan tangki. Selain itu, rumus ini juga digunakan dalam perhitungan hidrostatika, seperti tekanan dan gaya apung.

Rumus volume tabung pertama kali dikembangkan oleh Archimedes, seorang matematikawan Yunani kuno, sekitar abad ke-3 SM. Archimedes menggunakan rumus ini untuk menghitung volume mahkota raja, yang terbuat dari emas dan perak. Penemuan ini menjadi salah satu kontribusi terpenting Archimedes dalam bidang matematika.

Rumus Volume Tabung

Rumus V = rt merupakan persamaan penting untuk menghitung volume benda berbentuk tabung. Rumus ini memiliki beberapa aspek penting, antara lain:

Konstanta (pi)
Jari-jari alas (r)
Tinggi tabung (t)
Satuan volume (V)
Aplikasi dalam teknik
Aplikasi dalam fisika
Sejarah penemuan
Relevansi dalam matematika

Konstanta adalah bilangan irasional yang nilainya sekitar 3,14. Jari-jari alas dan tinggi tabung adalah besaran yang menentukan ukuran tabung. Satuan volume yang digunakan biasanya adalah cm atau m. Rumus volume tabung banyak digunakan dalam bidang teknik, seperti untuk menghitung volume pipa atau tangki. Dalam fisika, rumus ini digunakan untuk menghitung gaya apung dan tekanan hidrostatik. Penemuan rumus volume tabung oleh Archimedes merupakan tonggak sejarah dalam matematika. Rumus ini juga memiliki relevansi yang luas dalam matematika, seperti dalam kalkulus dan geometri.

Konstanta (pi)

Konstanta (pi) merupakan sebuah bilangan irasional yang nilainya sekitar 3,14. Konstanta ini memiliki peran penting dalam rumus volume tabung, yaitu V = rt. Dalam rumus ini, berfungsi sebagai pengali jari-jari alas dan tinggi tabung untuk menentukan volume tabung.

Konstanta merupakan komponen penting dalam rumus volume tabung karena menentukan bentuk tabung. Tanpa , volume tabung tidak dapat dihitung dengan akurat. Konstanta ini juga memiliki nilai yang sama untuk semua tabung, terlepas dari ukuran atau bentuknya.

Pemahaman tentang hubungan antara konstanta dan rumus volume tabung sangat penting dalam berbagai bidang, seperti teknik, fisika, dan matematika. Dalam teknik, rumus volume tabung digunakan untuk menghitung volume benda-benda berbentuk tabung, seperti pipa, kaleng, dan tangki. Dalam fisika, rumus ini digunakan untuk menghitung gaya apung dan tekanan hidrostatik. Dalam matematika, merupakan sebuah konstanta penting yang digunakan dalam berbagai perhitungan, seperti kalkulus dan geometri.

Jari-jari Alas (r)

Jari-jari alas (r) merupakan salah satu komponen penting dalam rumus V = rt. Jari-jari alas menentukan ukuran alas tabung, yaitu lingkaran. Semakin besar jari-jari alas, semakin besar pula luas alas tabung.

Dalam rumus V = rt, jari-jari alas berinteraksi dengan tinggi tabung (t) untuk menentukan volume tabung. Volume tabung akan berbanding lurus dengan jari-jari alas. Artinya, jika jari-jari alas diperbesar, maka volume tabung juga akan membesar. Hubungan ini sangat penting dalam aplikasi praktis rumus volume tabung.

Sebagai contoh, dalam teknik, rumus volume tabung digunakan untuk menghitung volume pipa atau tangki. Jari-jari alas pipa atau tangki menentukan kapasitas volume yang dapat ditampung. Dalam fisika, jari-jari alas tabung juga menentukan gaya apung dan tekanan hidrostatik. Misalnya, kapal yang memiliki jari-jari alas lebih besar akan memiliki daya apung yang lebih besar dibandingkan kapal dengan jari-jari alas lebih kecil.

Dengan demikian, pemahaman tentang hubungan antara jari-jari alas dan rumus volume tabung sangat penting dalam berbagai bidang. Dengan memahami hubungan ini, kita dapat menghitung volume tabung dengan akurat dan menerapkannya dalam berbagai aplikasi praktis.

Tinggi tabung (t)

Tinggi tabung (t) merupakan komponen penting dalam rumus V = rt. Tinggi tabung menentukan jarak antara alas dan tutup tabung. Semakin tinggi tabung, semakin besar pula volume yang dapat ditampung.

Peranan tinggi tabung
Tinggi tabung berinteraksi dengan jari-jari alas (r) untuk menentukan volume tabung. Volume tabung akan berbanding lurus dengan tinggi tabung. Artinya, jika tinggi tabung diperbesar, maka volume tabung juga akan membesar.
Aplikasi dalam kehidupan nyata
Rumus volume tabung dengan mempertimbangkan tinggi tabung digunakan dalam berbagai aplikasi kehidupan nyata, seperti:
– Menghitung volume cairan dalam tabung reaksi
– Menentukan kapasitas tangki penyimpanan
– Mendesain pipa dengan volume tertentu
– Menganalisis gaya apung kapal
Implikasi dalam rumus V = rt
Tinggi tabung merupakan faktor penting dalam menentukan volume tabung. Tanpa memperhitungkan tinggi tabung, rumus V = rt tidak dapat digunakan untuk menghitung volume tabung dengan akurat.

Dengan demikian, pemahaman tentang hubungan antara tinggi tabung dan rumus V = rt sangat penting dalam berbagai bidang. Dengan memahami hubungan ini, kita dapat menghitung volume tabung dengan akurat dan menerapkannya dalam berbagai aplikasi praktis.

Satuan volume (V)

Satuan volume (V) merupakan komponen penting dalam rumus V = rt, yang digunakan untuk menghitung volume tabung. Satuan volume menunjukkan besaran ruang yang ditempati oleh suatu benda. Dalam konteks rumus volume tabung, satuan volume biasanya dinyatakan dalam satuan kubik, seperti sentimeter kubik (cm³) atau meter kubik (m³).

Satuan volume memiliki peran penting dalam rumus volume tabung karena menentukan hasil akhir perhitungan volume. Tanpa satuan volume, hasil perhitungan akan menjadi tidak bermakna dan tidak dapat digunakan untuk tujuan praktis.

Dalam kehidupan nyata, pemahaman tentang satuan volume dan rumus volume tabung sangat penting dalam berbagai aplikasi, seperti:

Menentukan kapasitas tangki penyimpanan cairan atau gas
Mendesain pipa dengan volume tertentu untuk mengalirkan fluida
Menghitung volume benda berbentuk tabung, seperti kaleng atau drum

Dengan memahami hubungan antara satuan volume dan rumus volume tabung, kita dapat menghitung volume tabung dengan akurat dan menerapkannya dalam berbagai bidang praktis.

Aplikasi dalam teknik

Rumus volume tabung memiliki peran penting dalam berbagai aplikasi teknik, seperti:

Perancangan pipa: Rumus volume tabung digunakan untuk menghitung volume pipa yang dibutuhkan untuk mengalirkan fluida dengan kapasitas tertentu.
Desain tangki penyimpanan: Rumus ini digunakan untuk menentukan volume tangki yang diperlukan untuk menyimpan cairan atau gas dengan kapasitas tertentu.
Analisis struktur: Rumus volume tabung digunakan untuk menghitung volume benda berbentuk tabung, seperti kolom dan silinder, yang penting untuk analisis kekuatan dan stabilitas struktur.

Pemahaman yang baik tentang rumus volume tabung sangat penting bagi para insinyur untuk merancang dan membangun struktur dan sistem yang aman dan efisien. Kesalahan dalam menghitung volume tabung dapat berdampak serius pada kinerja dan keamanan struktur atau sistem tersebut.

Aplikasi dalam fisika

Rumus volume tabung (V = rt) memiliki peran penting dalam berbagai aplikasi fisika, seperti:

Gaya apung
Rumus volume tabung digunakan untuk menghitung gaya apung yang bekerja pada benda yang terendam dalam fluida. Gaya apung sebanding dengan volume benda yang terendam, yang dapat dihitung menggunakan rumus volume tabung.
Tekanan hidrostatik
Rumus volume tabung digunakan untuk menghitung tekanan hidrostatik pada suatu titik dalam fluida. Tekanan hidrostatik sebanding dengan kedalaman titik tersebut dan kerapatan fluida. Volume tabung dapat digunakan untuk menghitung volume fluida yang berada di atas titik tersebut, yang kemudian digunakan untuk menghitung tekanan hidrostatik.
Kapasitas kalor
Rumus volume tabung digunakan untuk menghitung kapasitas kalor benda berbentuk tabung. Kapasitas kalor suatu benda sebanding dengan volume dan massa jenis benda tersebut. Volume tabung dapat digunakan untuk menghitung volume benda, yang kemudian digunakan untuk menghitung kapasitas kalor.

Pemahaman yang baik tentang rumus volume tabung sangat penting bagi para fisikawan untuk menganalisis dan memahami berbagai fenomena fisika. Kesalahan dalam menghitung volume tabung dapat berdampak pada akurasi hasil analisis dan pemahaman tentang fenomena fisika tersebut.

Sejarah Penemuan

Penemuan rumus volume tabung memiliki sejarah yang panjang dan menarik. Rumus ini pertama kali ditemukan oleh Archimedes, seorang matematikawan Yunani kuno, sekitar abad ke-3 SM. Legenda mengatakan bahwa Archimedes menemukan rumus ini ketika ia sedang mandi dan menyadari bahwa volume air yang tumpah sama dengan volume benda yang dicelupkan ke dalam air.

Penemuan Archimedes ini merupakan terobosan besar dalam matematika dan fisika. Sebelumnya, tidak ada metode yang diketahui untuk menghitung volume benda berbentuk tabung. Rumus Archimedes memberikan cara yang sederhana dan akurat untuk menghitung volume tabung, dan rumus ini telah digunakan selama berabad-abad untuk berbagai aplikasi praktis.

Pemahaman tentang sejarah penemuan rumus volume tabung sangat penting karena beberapa alasan. Pertama, hal ini membantu kita untuk menghargai kejeniusan Archimedes dan kontribusinya yang luar biasa pada matematika dan fisika. Kedua, hal ini menunjukkan pentingnya matematika dalam memecahkan masalah dunia nyata. Ketiga, hal ini menunjukkan bahwa bahkan penemuan matematika yang paling mendasar pun dapat memiliki dampak yang signifikan pada kehidupan kita sehari-hari.

Relevansi dalam matematika

Rumus volume tabung (V = rt) memiliki relevansi yang luas dalam matematika, karena digunakan dalam berbagai bidang, seperti kalkulus, geometri, dan statistika.

Kalkulus
Dalam kalkulus, rumus volume tabung digunakan untuk menghitung volume benda putar yang terbentuk dari rotasi bidang datar mengelilingi sumbu. Misalnya, rumus ini digunakan untuk menghitung volume bola, silinder, dan kerucut.
Geometri
Dalam geometri, rumus volume tabung digunakan untuk menghitung volume benda-benda berbentuk tabung, seperti pipa, kaleng, dan tangki. Rumus ini juga digunakan untuk menghitung luas permukaan benda-benda tersebut.
Statistika
Dalam statistika, rumus volume tabung digunakan untuk menghitung distribusi probabilitas variabel acak yang mengikuti distribusi normal. Rumus ini juga digunakan untuk menghitung nilai harapan dan varians dari variabel acak tersebut.

Pemahaman tentang relevansi rumus volume tabung dalam matematika sangat penting karena memungkinkan kita untuk menggunakan rumus ini untuk memecahkan berbagai masalah matematika dan untuk memahami konsep-konsep matematika yang lebih kompleks.

Pertanyaan Umum tentang Rumus Volume Tabung

Berikut adalah beberapa pertanyaan umum tentang rumus volume tabung beserta jawabannya:

Pertanyaan 1: Apa saja komponen dalam rumus volume tabung?

Jawaban: Rumus volume tabung (V = rt) terdiri dari tiga komponen: (konstanta pi), r (jari-jari alas tabung), dan t (tinggi tabung).

Pertanyaan 2: Bagaimana cara menggunakan rumus volume tabung?

Jawaban: Untuk menggunakan rumus volume tabung, substitusikan nilai (sekitar 3,14), jari-jari alas tabung (r), dan tinggi tabung (t) ke dalam rumus. Hasilnya adalah volume tabung dalam satuan kubik.

Pertanyaan 3: Apa saja aplikasi rumus volume tabung?

Jawaban: Rumus volume tabung memiliki berbagai aplikasi, antara lain dalam teknik (misalnya menghitung volume pipa atau tangki), fisika (misalnya menghitung gaya apung atau tekanan hidrostatik), dan matematika (misalnya menghitung volume benda putar).

Pertanyaan 4: Siapa yang menemukan rumus volume tabung?

Jawaban: Rumus volume tabung pertama kali ditemukan oleh Archimedes, seorang matematikawan Yunani kuno, sekitar abad ke-3 SM.

Pertanyaan 5: Mengapa rumus volume tabung penting?

Jawaban: Rumus volume tabung penting karena memungkinkan kita untuk menghitung volume benda berbentuk tabung secara akurat. Rumus ini memiliki banyak aplikasi dalam berbagai bidang, seperti teknik, fisika, dan matematika.

Pertanyaan 6: Apa saja keterbatasan rumus volume tabung?

Jawaban: Rumus volume tabung hanya berlaku untuk benda berbentuk tabung yang memiliki alas berbentuk lingkaran. Untuk benda dengan bentuk lain, diperlukan rumus yang berbeda untuk menghitung volumenya.

Dengan memahami rumus volume tabung dan aplikasinya, kita dapat memecahkan berbagai masalah yang melibatkan benda berbentuk tabung.

Artikel selanjutnya akan membahas tentang teknik menghitung volume tabung dengan menggunakan rumus V = rt.

Tips Menggunakan Rumus Volume Tabung

Rumus volume tabung (V = rt) merupakan persamaan matematika yang penting untuk menghitung volume benda berbentuk tabung. Berikut beberapa tips untuk menggunakan rumus volume tabung secara efektif:

Tip 1: Pahami Komponen Rumus

Rumus V = rt terdiri dari tiga komponen, yaitu (konstanta pi), r (jari-jari alas tabung), dan t (tinggi tabung). Pastikan Anda memahami arti dari masing-masing komponen ini sebelum menggunakan rumus.

Tip 2: Gunakan Satuan yang Konsisten

Saat menggunakan rumus volume tabung, pastikan Anda menggunakan satuan yang konsisten. Misalnya, jika jari-jari alas tabung diukur dalam sentimeter, maka tinggi tabung dan volume tabung juga harus diukur dalam sentimeter.

Tip 3: Perhatikan Tanda Negatif

Dalam beberapa kasus, tinggi tabung mungkin bernilai negatif. Hal ini dapat terjadi ketika tabung diukur dari titik referensi yang berbeda. Jika tinggi tabung bernilai negatif, pastikan Anda memasukkan tanda negatif ke dalam rumus.

Tip 4: Gunakan Kalkulator yang Akurat

Konstanta adalah bilangan irasional yang tidak dapat dinyatakan sebagai pecahan sederhana. Oleh karena itu, disarankan untuk menggunakan kalkulator yang akurat saat menghitung volume tabung.

Tip 5: Periksa Hasil Anda

Setelah menghitung volume tabung, periksa kembali hasil Anda. Anda dapat melakukan ini dengan menggunakan metode lain untuk menghitung volume, seperti mengukur volume secara langsung atau menggunakan simulasi komputer.

Dengan mengikuti tips-tips ini, Anda dapat menggunakan rumus volume tabung secara efektif dan akurat untuk menghitung volume benda berbentuk tabung.

Kesimpulan

Rumus volume tabung (V = rt) merupakan persamaan matematika yang sangat penting untuk menghitung volume benda berbentuk tabung. Rumus ini memiliki berbagai aplikasi dalam berbagai bidang, seperti teknik, fisika, dan matematika. Pemahaman yang baik tentang rumus volume tabung sangat penting untuk dapat menyelesaikan masalah yang melibatkan benda berbentuk tabung secara akurat.

Dengan semakin berkembangnya teknologi, diharapkan akan ditemukan metode-metode baru yang lebih akurat dan efisien untuk menghitung volume tabung. Namun, rumus volume tabung yang telah kita bahas dalam artikel ini akan tetap menjadi dasar yang penting untuk memahami konsep volume tabung dan aplikasinya.